
Transformation of velocities
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 16
الجزء والصفحة:
Volume I, Chapter 16
 2024-02-25
2024-02-25
 2015
2015
The main difference between the relativity of Einstein and the relativity of Newton is that the laws of transformation connecting the coordinates and times between relatively moving systems are different. The correct transformation law, that of Lorentz, is

These equations correspond to the relatively simple case in which the relative motion of the two observers is along their common x-axes. Of course, other directions of motion are possible, but the most general Lorentz transformation is rather complicated, with all four quantities mixed up together. We shall continue to use this simpler form, since it contains all the essential features of relativity.
Let us now discuss more of the consequences of this transformation. First, it is interesting to solve these equations in reverse. That is, here is a set of linear equations, four equations with four unknowns, and they can be solved in reverse, for x,y,z,t in terms of x′,y′,z′,t′. The result is very interesting, since it tells us how a system of coordinates “at rest” looks from the point of view of one that is “moving.” Of course, since the motions are relative and of uniform velocity, the man who is “moving” can say, if he wishes, that it is really the other fellow who is moving and he himself who is at rest. And since he is moving in the opposite direction, he should get the same transformation, but with the opposite sign of velocity. That is precisely what we find by manipulation, so that is consistent. If it did not come out that way, we would have real cause to worry!

Next, we discuss the interesting problem of the addition of velocities in relativity. We recall that one of the original puzzles was that light travels at 186,000 mi/sec in all systems, even when they are in relative motion. This is a special case of the more general problem exemplified by the following. Suppose that an object inside a space ship is going at 100,000 mi/sec and the space ship itself is going at 100,000 mi/sec; how fast is the object inside the space ship moving from the point of view of an observer outside? We might want to say 200,000 mi/sec, which is faster than the speed of light. This is very unnerving, because it is not supposed to be going faster than the speed of light! The general problem is as follows.
Let us suppose that the object inside the ship, from the point of view of the man inside, is moving with velocity v, and that the space ship itself has a velocity u with respect to the ground. We want to know with what velocity vx this object is moving from the point of view of the man on the ground. This is, of course, still but a special case in which the motion is in the x-direction. There will also be a transformation for velocities in the y-direction, or for any angle; these can be worked out as needed. Inside the space ship the velocity is vx′, which means that the displacement x′ is equal to the velocity times the time:

Now we have only to calculate what the position and time are from the point of view of the outside observer for an object which has the relation (16.2) between x′ and t′. So, we simply substitute (16.3) into (16.2), and obtain

But here we find x expressed in terms of t′. In order to get the velocity as seen by the man on the outside, we must divide his distance by his time, not by the other man’s time! So we must also calculate the time as seen from the outside, which is

the square roots having cancelled. This is the law that we seek: the resultant velocity, the “summing” of two velocities, is not just the algebraic sum of two velocities (we know that it cannot be or we get in trouble), but is “corrected” by 1+uv/c2.
Now let us see what happens. Suppose that you are moving inside the space ship at half the speed of light, and that the space ship itself is going at half the speed of light. Thus u is 1/2c and v is 1/2c, but in the denominator uv/c2 is one-fourth, so that

So, in relativity, “half” and “half” does not make “one,” it makes only “4/5.” Of course, low velocities can be added quite easily in the familiar way, because so long as the velocities are small compared with the speed of light we can forget about the (1+uv/c2) factor; but things are quite different and quite interesting at high velocity.
Let us take a limiting case. Just for fun, suppose that inside the space ship the man was observing light itself. In other words, v=c, and yet the space ship is moving. How will it look to the man on the ground? The answer will be

Therefore, if something is moving at the speed of light inside the ship, it will appear to be moving at the speed of light from the point of view of the man on the ground too! This is good, for it is, in fact, what the Einstein theory of relativity was designed to do in the first place—so it had better work!
Of course, there are cases in which the motion is not in the direction of the uniform translation. For example, there may be an object inside the ship which is just moving “upward” with the velocity vy′ with respect to the ship, and the ship is moving “horizontally.” Now, we simply go through the same thing, only using y’s instead of x’s, with the result
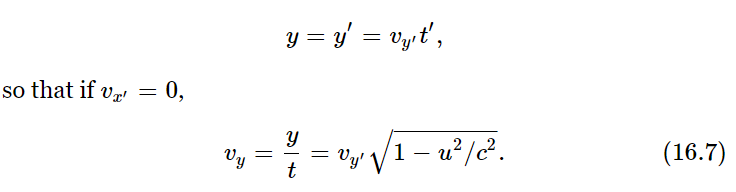
Thus a sidewise velocity is no longer vy′, but  We found this result by substituting and combining the transformation equations, but we can also see the result directly from the principle of relativity for the following reason (it is always good to look again to see whether we can see the reason). We have already (Fig. 15–3) seen how a possible clock might work when it is moving; the light appears to travel at an angle at the speed c in the fixed system, while it simply goes vertically with the same speed in the moving system. We found that the vertical component of the velocity in the fixed system is less than that of light by the factor
We found this result by substituting and combining the transformation equations, but we can also see the result directly from the principle of relativity for the following reason (it is always good to look again to see whether we can see the reason). We have already (Fig. 15–3) seen how a possible clock might work when it is moving; the light appears to travel at an angle at the speed c in the fixed system, while it simply goes vertically with the same speed in the moving system. We found that the vertical component of the velocity in the fixed system is less than that of light by the factor 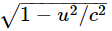 (see Eq. 15.3). But now suppose that we let a material particle go back and forth in this same “clock,” but at some integral fraction 1/n of the speed of light (Fig. 16–1). Then when the particle has gone back and forth once, the light will have gone exactly n times. That is, each “click” of the “particle” clock will coincide with each nth “click” of the light clock. This fact must still be true when the whole system is moving, because the physical phenomenon of coincidence will be a coincidence in any frame. Therefore, since the speed cy is less than the speed of light, the speed vy of the particle must be slower than the corresponding speed by the same square-root ratio! That is why the square root appears in any vertical velocity.
(see Eq. 15.3). But now suppose that we let a material particle go back and forth in this same “clock,” but at some integral fraction 1/n of the speed of light (Fig. 16–1). Then when the particle has gone back and forth once, the light will have gone exactly n times. That is, each “click” of the “particle” clock will coincide with each nth “click” of the light clock. This fact must still be true when the whole system is moving, because the physical phenomenon of coincidence will be a coincidence in any frame. Therefore, since the speed cy is less than the speed of light, the speed vy of the particle must be slower than the corresponding speed by the same square-root ratio! That is why the square root appears in any vertical velocity.

Fig. 16–1. Trajectories described by a light ray and particle inside a moving clock.
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


