Died: 5 February 1977 in Stockholm, Sweden

Oskar Klein was was the youngest son of Sweden' s first rabbi, Gottlieb Klein, who was originally from the Southern Carpathian. Gottlieb Klein received his doctorate from Heidelberg and moved to Sweden in 1883. He evidently instilled an interest in learning in his young son, as Oskar became quite fond of biology at an early age. This interest changed to chemistry around the age of 15 and soon after, in 1910, Svante Arrhenius, at what seems to be the behest of Gottlieb, invited Oskar to work in his laboratory at the Nobel Institute. Here he took up an interest in solubility and he published his first paper in 1912 on the solubility of zinc hydroxide in alkalis. This was the very same year that he finished his secondary education. He waited, however, until 1914 to take the University exam.

Arrhenius wanted to send Klein to work with Jean-Baptiste Perrin in his laboratory at the University of Paris but the plan was foiled by the outbreak of World War I. Klein found himself caught up in the tempest and saw military service in 1915 and 1916. After his service concluded, but with the war still raging, he returned to work with Arrhenius.

Their work now centred around studying dielectric constants of alcohols in various solvents. During this particular stay in Stockholm, he met Hendrik A Kramers, who, at the time (1917), was a student of Niels Bohr in Copenhagen. Kramers and Klein met several times during the next few years both in Stockholm and in Copenhagen, which was to be Klein's next destination.

In 1917 Klein received a fellowship to study abroad and, subsequently, arrived in Copenhagen in 1918. Over the course of the next two years he would travel between Stockholm and Copenhagen performing work for both Bohr and Arrhenius, spending the summer of 1919 with Kramers in Copenhagen, and finally returning to Stockholm in 1920. But that was not to be the end of his Copenhagen experience. In fact, it was merely the beginning.

Bohr traveled to Stockholm in 1920 to visit Klein and convinced him to return to Copenhagen once more to work at Bohr's Institute. Klein agreed and began what would prove to be quite a fruitful relationship that eventually would lead him to his first teaching position.

Around this time, Bohr was working with Svein Rosseland on the statistical equilibrium of a mixture of atomic and free electrons. At the time, it was believed that electrons colliding with atoms always lost energy. However, Klein, in conjunction with Rosseland, introduced "collisions of the second kind" where the electrons actually gained energy!

Klein continued his work on the other side of the 'molecular aisle' by turning his attention to ions. In fact, this led him to his thesis research in which he studied the forces between ions in strong electrolytes using Gibbs' statistical mechanics. The result was a generalized formulation of Brownian motion. He defended his doctorate in 1921 at Stockholm Högskola and was opposed by Erik Ivar Fredholm the mathematical physicist best known for his work on integral equations and spectral theory. After his successful defence, Klein returned to Copenhagen, later assisting Bohr on a trip to Göttingen.

Around this time Klein turned to publishing semi-popular writings on physics. His first work in this new arena was a philosophical paper that was a refutation of an objection to relativity theory by Swedish philosophers. Not surprisingly, it was around this time that he began to look for a job.

In 1923, Oskar Klein married Gerda Agnete Koch and moved to Ann Arbor, Michigan to take up a post at the University of Michigan, a post he won with no small thanks to his venerable friend Niels Bohr. His first work in Ann Arbor dealt with the anomalous Zeeman effect which was a problem that arose out of the fact that no one at the time understood the behavior of atoms in a magnetic field. The classical Zeeman effect was explained, in a nutshell, as the splitting of spectral lines by the magnetic field. The problem was that the classical theory only effectively described atoms with a total electron spin of zero. The difference can be seen in the Hamiltonians of the two. For the normal Zeeman effect, the Hamiltonian reads:

H₁ = e/2mc L . B

For the anomalous Zeeman effect, the Hamiltonian becomes:

H₁ = e/2mc (L + 2S) . B

The extra term arises from the intrinsic dipole moment of an object with spin, where S is the spin angular momentum. For the time (1923), this was a fairly large problem to tackle, but Klein did not stop there.

He went on to work on the interaction of diatomic molecules with precessing electrons, studying the angular momentum within the molecule itself. The following year, in 1924, he taught a course on electromagnetism and lectured on an electric particle in a combined gravitational and electromagnetic field. This was the beginning of his landmark work on a unified field theory.

Klein chose to solve the problem by essentially extending his work to a fifth dimension, though his early unification ideas centred around quantum physics as the catalyst. He did this by setting p₅² = m². Brink [5] has said that Klein was driven by:-

... the wish to have a formalism which includes the wave aspect and the particle aspect as a limit.

After a time Klein argued less and less that quantum physics could lead to a unified picture, in fact he later abandoned the idea entirely. However, he did see the possibility of unification in five dimensions, which seems to have been present in his initial attempt.

At this time, Klein apparently was unaware of the work of Theodor Kaluza. Kaluza, in 1919, sent a paper to Albert Einstein proposing a unification of gravity with Maxwell's theory of light. Einstein initially was uninterested in the paper, but later realized the highly original ideas contained within it and encouraged Kaluza to publish his ideas. In fact the paper was communicated by Einstein himself on 8 December 1921.

In 1925, Klein returned to Copenhagen and contracted hepatitis. He was ill for half a year, though he was visited by Heisenberg in July of 1925 and Schrödinger in January of 1926. This was around the time he was finally able to return to work. It was at this time that he finally became aware of Kaluza's work. Wolfgang Pauli communicated this work to him and Klein:-

... tried to rescue what I could from the shipwreck.

Klein's adaptation of Kaluza's work had a major difference from the original in that the extra or fifth dimension was curled up into a ball that was on the order of the Planck length, 10^-33 cm. It is important to note, however, that the extra dimension, though curled up, was still Euclidean in nature. Basically, the fifth coordinate was not observable but was a physical quantity that was conjugate to the electrical charge. As Kragh [4] explains, Klein attempted to explain the atomicity of electricity as a quantum law. He also attempted to account for the electron and the proton.

Klein assumed the fifth dimension to be periodic with a period l = c(2k)^1/2/e where e was the charge of the electron and k was Einstein's constant of gravitation. The dimension was on the order of the Planck length.

Klein's results were published in Nature in the autumn of 1926 and generated interest from such eminent theorists as Vladimir Fock, Leon Rosenfeld, Louis de Broglie, and Dirk Struik. Unfortunately, despite a lot of initial interest in unification, most physicists eventually went on to more promising and experimentally testable research leaving Kaluza-Klein theory to be explored by another generation of physicists nearly half a century later. In Klein's own words:-

Dirac may well say that my main trouble came from trying to solve too many problems at a time.

It was also in 1926 that Klein was appointed as docent at Lund University and became, for the next five years, Bohr's closest collaborator both on correspondence and complimentarity, and apparently contributed to the development of the uncertainty principle, as Heisenberg recalled:-

After several weeks of discussion, which were not devoid of stress, we soon concluded, not least thanks to Oskar Klein's participation, that we really meant the same, and that the uncertainty relations were just a special case of the more general complementarity principle.

In fact, 1926 was a banner year for Klein. In addition to finally recovering from the hepatitis and becoming docent at Lund, it was in this same year that he made his next great theoretical breakthrough. In a paper in which he determined the atomic transition probabilities (prior to Dirac), he introduced the initial form of what would become known as the Klein-Gordon equation.

The Klein-Gordon equation was the first relativistic wave equation. The equation can be written:

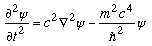
It is interesting to note that this equation appeared exactly as it has been written in David Bohm's 1951 book Quantum Theory but was not called the Klein-Gordon equation. However, Bethe and Jackiw's Intermediate Quantum Mechanics, originally written in 1964, does refer to the same equation as the Klein-Gordon equation. Klein and Walter Gordon were thus eventually honoured with having the equation named after them, though it seems to have taken over a quarter of a century to receive the honour. Oddly enough, Schrödinger himself privately developed a relativistic wave equation from his original wave equation, which, in reality, was not that difficult to do, and did so prior to Klein and Gordon, though he never published his results. The trouble came when the equation did not result in the correct fine structure of the hydrogen atom and when Pauli introduced the concept of spin a year later (1927). The equation turned out to be incompatible with spin and, as a result, is only useful for calculations involving spinless particles. But, nonetheless, it was an important point in quantum theory and, along with his unification theory, was to ensure a lasting legacy for Klein and cemented 1926 as a pivotal year in his life.

In the years following 1926, Klein turned to teaching and continued his research, though possibly at a reduced pace. Brink [5] quotes a friend and mentor to Klein as having said:-

You will now fulfill the words: go and teach the people. Your great pedagogical talents always were one of your strongest qualities. I am not of the opinion that finding new laws of nature and indicating new directions is one of your great strengths, although you always have developed a certain ambition in this direction.

In 1927, Klein was appointed Lektor in Copenhagen but nonetheless continued his research working with Pascual Jordan on the second quantization in quantum mechanics.

In his work with Jordan, he demonstrated the close connection between quantum fields and quantum statistics. It was known that second quantization guarantees that photons obey Bose-Einstein statistics, but Klein showed that second quantization is not confined to free particles only. He and Jordan showed that one can quantize the non-relativistic Schrödinger equation and, in honour of this work, he was the recipient of yet another named mathematical tool, the Jordan-Klein matrices.

In subsequent years he collaborated with the Japanese physicist Yoshio Nishina who was in Copenhagen on an extended research visit and worked on the problem of Compton scattering of a Dirac electron. Despite the so-called Klein paradox, that being that the positron was not completely understood by physicists, he was able to convince physicists of the soundness of Dirac's relativistic wave equation. His continued work included the quantum mechanics of the second law of thermodynamics and Klein's lemma.

In 1930, he was offered Fredholm's position at Stockholm Högskala and he finally returned to his native city to take up a post that he held until his retirement in 1962.

During the 1930s, Klein helped many refugee physicists who were expelled from Germany and other nations largely due to their Jewish heritage. Of the many he helped, one included Walter Gordon who would later join Klein in being the beneficiaries of the named equation we have just discussed. In 1943, Klein also aided in Bohr's escape from Copenhagen.

During the 1930s Klein also found time to attend conferences, not the least of which included the 1938 Warsaw Conference where he spoke on (almost) non-Abelian gauge theories. This conference included some of the leading theorists of the day including Sir Arthur Eddington, Eugene Wigner, and others. It was at this conference that Klein suggested that a spin -1 particle mediated beta decay and played a role in weak interactions in a similar manner to the photon in electromagnetism. Klein's hypothesis was yet another crack at a unified field theory, this time in attempt to unify the strong, weak, and electromagnetic forces. The work was not noticed until nearly twenty years later when it was resurrected by Julian Schwinger in 1957.

In the 1940s Klein worked on a wide variety of subjects including superconductivity (with Jens Lindhard in 1945), biochemistry, universal p-decay, general relativity, and stellar evolution. Sometime after 1947 he, and independently Giovanni Puppi, realized that both the electron and the -meson were "weak" particles.

In the 1950s and 1960s Klein remained active, addressing the 11^th Solvay Conference in 1958, developing a new model for cosmology in conjunction with Hannes Alfven in 1963, and tackling Einstein's General Relativity in a paper published in Astrophisica Norvegica in 1964. During his later years, he also became very interested in philosophy and especially in analogies between science and religion. In addition, he took to writing a few popular books, most of which are out of print.

Books:

1. Bethe and R Jackiw, Intermediate Quantum Mechanics (Reading, 1997).

Articles:

1. Klein, Some General Aspects of Einstein's Theory of Relativity, Astophysica Norvegica 9 (1964) 161-169.