Concept of the Hole

In considering the two-dimensional representation of the covalent bonding a positively charged "empty state" was created when a valence electron was elevated into the conduction band. For T > 0 K, all valence electrons may gain thermal energy; if a valence electron gains a small amount of thermal energy, it may hop into the empty state. The movement of a valence electron into the empty state is equivalent to the movement of the positively charged empty state itself. Figure 1.1 shows the

movement of valence electrons in the crystal alternately filling one empty state and creating a new empty state, a motion equivalent to a positive charge moving in the valence band. The crystal now has a second equally important charge carrier that can give rise to a current. This charge carrier is called a hole and, as we will see, can also be thought of as a classical particle whose motion can be modeled using Newtonian mechanics.

The drift current density due to electrons in the valence band, can be written as

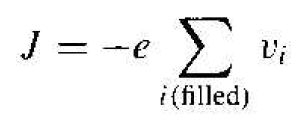(1)

where the summation extends over all filled states. This summation is inconvenient since it extends over a nearly full valence band and takes into account a very large number of states. We may rewrite Equation (1) in the form

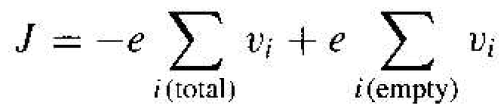(2)

If we consider a band that is totally full, all available states are occupied by electrons.

The individual electrons can be thought of as moving with a velocity as given by Equation 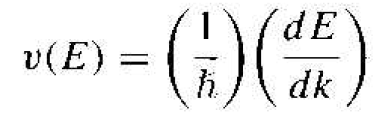(3):

(3)

The band is symmetric in k and each state is occupied so that, for every electron with a velocity |v| , there is a corresponding electron with a velocity -|v|. Since the band is full, the distribution of electrons with respect to k cannot he changed with an externally applied force. The net drift current density generated from a completely full

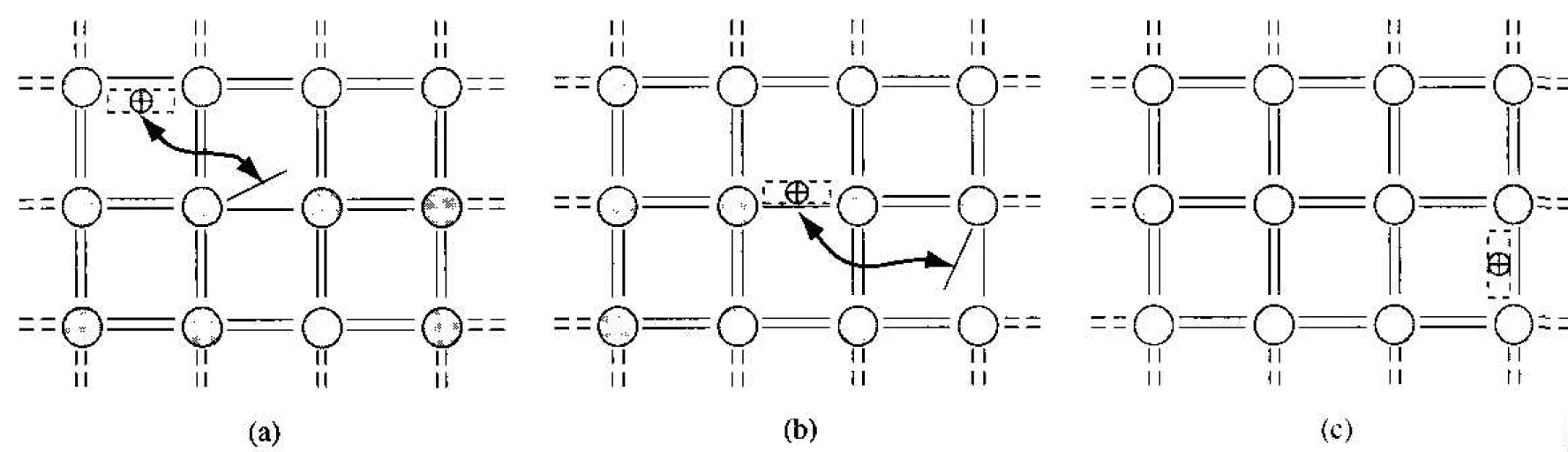
Figure 1.1 Visualization of the movement of a hole in a semiconductor.

band, then, is zero, or

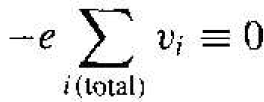(4)

We can now write the drift current density from Equation (3) for an almost full band as

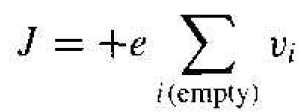(5)

where the v_i in the summation is the

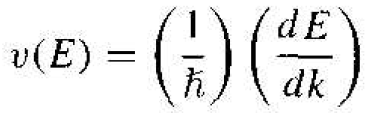
associated with the empty state. Equation (5) is entirely equivalent to placing a positively charged particle in the empty states and assuming all other states in the hand are empty, or neutrally charged. This concept is shown in Figure 1.2. Figure 1.2a shows the valence band with the conventional electron-filled states and empty states, while Figure 1.2b shows the new concept of positive charges occupying the original empty states. This concept is consistent with the discussion of the positively charged empty state" in the valence band as shown in Figure 1.1.

The v_i in the summation of Equation (5) is related to how well this positively charged panicle moves in the semiconductor. Now consider an electron near the top of

the allowed energy. The energy near the top of the allowed energy band may again he approximated by a parabola so that we may write

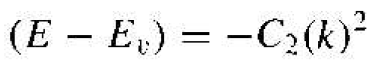(6)

The energy E,, is the energy at the top of the energy band. Since E < E_v for electrons in this band, then the parameter C₂ must be a positive quantity.

Taking the second derivative of E with respect to k from Equation (6), we obtain

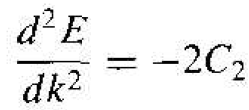(7)

We may rearrange this equations o that

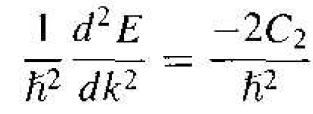(8)

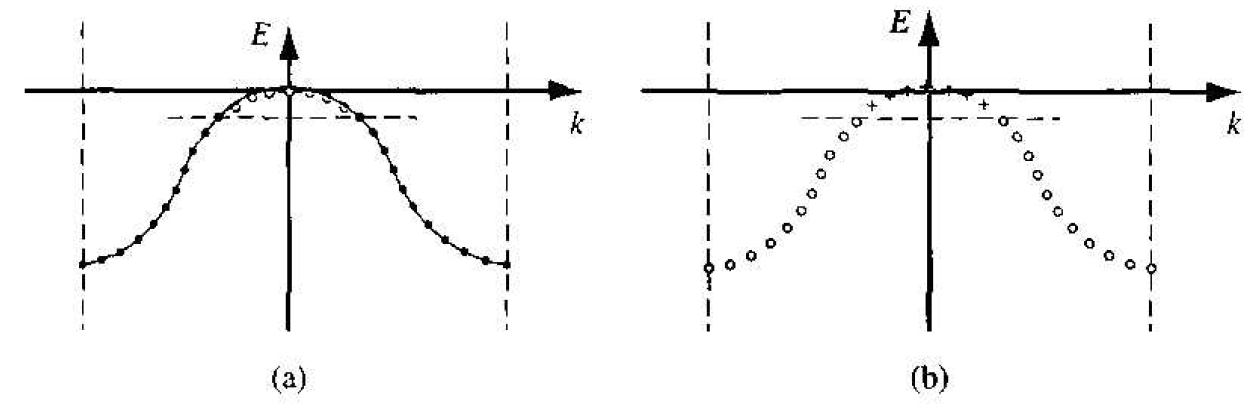
Figure 1.2 (a) Valence band with conventional electron-filled sates and empty states (b) Concept of positive charges occupying the original empty states.

Comparing Equation (8), we may write

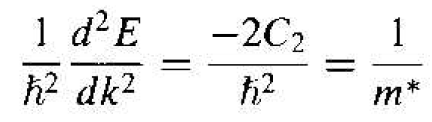(9)

where m^* is again an effective mass. We have argued that C₂ is a positive quantity, which now implies that m^* is a negative quantity. An electron moving near the top of an allowed energy band behaves as if it has a negative mass.

We must keep in mind that the effective mass parameter is used to relate quantum mechanics and classical mechanics. The attempt to relate these two theories leads to this strange result of a negative effective mass. However, we must recall that solutions to Schrodinger's wave equation also led to results that contradicted classical mechanics. The negative effective mass is another such example.

In discussing the concept of effective mass in the last section, we used an analogy of marbles moving through two liquids. Now consider placing an ice cube in the center of a container filled with water: the ice cube will move upward toward the surface in a direction opposite to the gravitational force. The ice cube appears to have a negative effective mass since its acceleration is opposite to the external force. The effective mass parameter takes into account all internal forces acting on the particle.

If we again consider an electron near the top of an allowed energy band and use Newton's force equation for an applied electric field, we will have

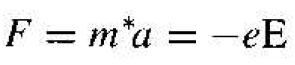(10)

However, m^* is now a negative quantity, so we may write

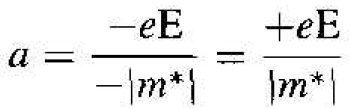(11)

An electron moving near the top of an allowed energy band moves in the same direction as the applied electric field.

The net motion of electrons in a nearly full band can be described by considering just the empty states, provided that a positive electronic charge is associated with each state and that the negative of m* from Equation (9) is associated with each state. We now can model this band as having particles with a positive electronic charge and a positive effective mass. The density of these panicles in the valence band is the same as the density of empty electronic energy states. This new panicle is the hole. The hole, then, has a positive effective mass denoted by m^*_p and a positive electronic charge, so it will move in the same direction as an applied field.