


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2019
Date: 23-1-2019
Date: 4-3-2019
|
What is an exponential function?
An exponential function is a mathematical expression in which a variable represents the exponent of an expression.
What does an exponential function look like?
Here's a very simple exponential function:
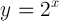
That equation is read as "y equals 2 to the x power."
Exponent refresher:
Let's remember how exponents work. Suppose we have the equation below:
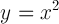
That equation tells us to multiply x by itself to get y. It's the equivalent of:

If we want to find y when x=3, we can pretty quickly find that y=3*3=9. But, this is actually what's known as a "power function". In fact, it's just a polynomial, and not an exponential function at all.
Take a closer look at x2 . This means x squared or x to the second power. What does it mean? There are two parts to this exponential term:
1) An exponent, which is the number 2.
2) A base, which is the variable x.
With exponential functions, the variable will actually be the exponent, with a constant as the base.
Exponential Functions
Here's what exponential functions look like:
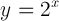
The equation is y equals 2 raised to the x power. This sort of equation represents what we call "exponential growth" or "exponential decay." Other examples of exponential functions include:

The general exponential function looks like this:  , where the base b is any positive constant. The base b could be 1, but remember that 1 to any power is just 1, so it's a particularly boring exponential function!
, where the base b is any positive constant. The base b could be 1, but remember that 1 to any power is just 1, so it's a particularly boring exponential function!
Let's try some examples:
Example 1
Solve for x: 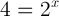
This one is actually pretty simple, so let's just think it through:
The problem says we have to multiply x number of two's together to get four. Well, everyone knows that 2*2=4, so the answer is two:
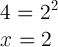
Ok, great, that was an easy example. But you can see where this could get really, hard, right? Look at this:
Example 2
Solve for y when x=5.
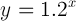
That means we need to plug-in x=5 and see what we get:
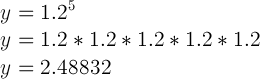
Fortunately all we had to do with this problem was multiply 1.2 times itself a few times to get the answer.
What about a word problem example?
We can use a formula for exponential growth to model the population of a bacteria. Let's say the bacteria population is defined by 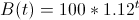 where B is the total population and t represents time in hours. While that may look complicated, it really tells us that the bacteria grows by 12 percent every hour. Every time another hour goes by, t goes up by 1, so we have to multiply the population times 1.12 again. The 100 simply sets the initial population at time t=0.
where B is the total population and t represents time in hours. While that may look complicated, it really tells us that the bacteria grows by 12 percent every hour. Every time another hour goes by, t goes up by 1, so we have to multiply the population times 1.12 again. The 100 simply sets the initial population at time t=0.
So, how much bacteria remains after 4 hours?
What do we know? We have the formula 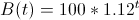 and the fact that t=4.
and the fact that t=4.
Replace t with 4 hours in the formula above and simplify.
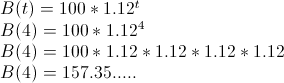



|
|
|
|
كل ما تود معرفته عن أهم فيتامين لسلامة الدماغ والأعصاب
|
|
|
|
|
|
|
ماذا سيحصل للأرض إذا تغير شكل نواتها؟
|
|
|
|
|
|
|
جامعة الكفيل تناقش تحضيراتها لإطلاق مؤتمرها العلمي الدولي السادس
|
|
|