


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-11-2016
Date: 22-11-2016
Date: 24-11-2016
|
Differentiation and Integration in RN-The Riemann Integral in RN
The method of extending the Riemann integral from R1 to RN is similar to the extension of the Darboux integral described in Section of (The Darboux Integral in RN)
Definitions
Let A be a set in a metric space S with metric d. We define the diameter of A as the sup d(x, y), where the supremum is taken over all x, y in A. The notation diam A is used for the diameter of A. Suppose that F isa domain in RN and that Δ ={F1,F2,...,Fn} is a subdivision of F. The mesh of Δ, denoted by Δ, is the maximum of the diameters of F1,F2,...,Fn.
Definition
Let f be a function from F, a domain in RN into R1. Then f is Riemann integrable on F if there is a number L with the following property: For each ε> 0 there is a δ> 0 such that if Δ is any subdivision of F with Δ<δ, and xi∈ Fi , i = 1, 2,...,n, then
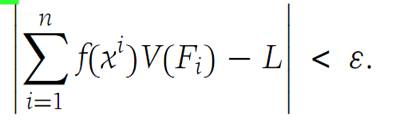
This inequality must hold no matter how the xi are chosen in the Fi . The number L is called the Riemann integral of over , and we use the notation
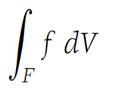
for this value.
We recall that in R1 the Darboux and Riemann integrals are the same. The next two theorems state that the same result holds for integrals in RN.
Theorem 1.1
Let F be a domain in RN and suppose that f :F → R1 is Riemann integrable on F. Then f is Darboux integrable on F, and the two integrals are equal. The converse of Theorem 1.1 is contained in the following result.
Theorem 1.2
Let F be a domain in RN and suppose that f :F → R1 is bounded on F. Then
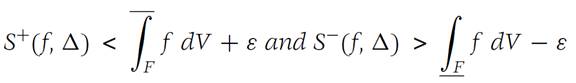
for every subdivision of mesh ||Δ||<δ;
(b) if f is Darboux integrable on F, then it is Riemann integrable on F, and
the integrals are equal.
Proof
Observe that (b) is an immediate consequence of (a), since each Riemann sum is between S−(f,Δ) and S+(f,Δ).Hence, if
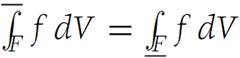
This value is also the value of the Riemann integral.
We shall prove only the first inequality in (1.1), because the proof of the second is similar.
Since f is bounded, there is a number M such that |f(x)|≤ M for all x ∈ F. Let ε> 0 be given. According to the definition of upper Darboux integral, there is a subdivision Δ0 ={F1,F2,...,Fm} such that(1.2)
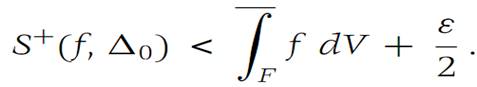
Define F(0)I to be the set of interior points of Fi . It may happen that F(0)I is empty for some values of i. For each F(0)I that is not empty, we select a closed domain Gi contained in F(0)I such that
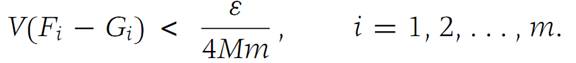
It is not difficult to verify that such closed domains G1,G2,...,Gm can always be found. For example, each Gi may be chosen as the union of closed hypercubes interior to Fi for a sufficiently small grid size.
Since each set Gi is closed and is contained in F(0)i, there is a positive number δ such that every ball B(x, δ) with x in some Gi has the property that B(x, δ) is contained in the corresponding set F(0)I . Let Δ be any sub division with mesh less than δ. We shall show that the first inequality in (1.2) holds for this subdivision.
We separate the domains of Δ into two classes: J1,J2,...,Jn are those domains Δ1 of Δ containing points of some Gi ; K1,K2,...,Kq are the remaining domains of Δ, denoted by Δ0. Denote by Δ0.
the common refinement of Δ1 and Δ0. Because of the manner in which we chose Δ, each Ji is contained entirely in some F(0)k . Therefore, J1,J2,...,Jn are domains in the refinement Δ/ . The remaining domains of Δ/ are composed of the sets Ki ∩ Fj , i = 1, 2,...,q; j = 1, 2,...,m. We have the inequality
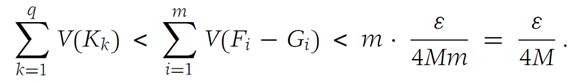
We introduce the notation
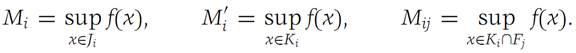
Using the definitions of S+(f,Δ) and S+(f,Δ/), we obtain
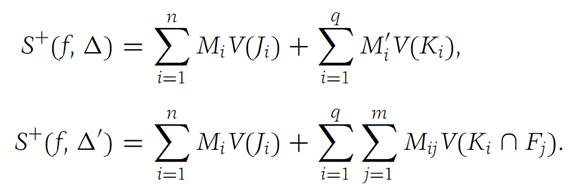
Now it is clear that
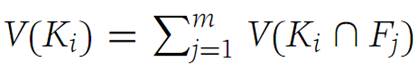
Therefore, by subtraction, it follows that
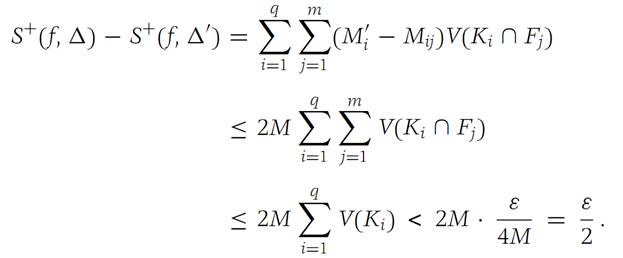
We have
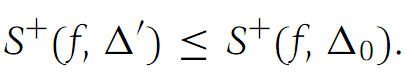
Combining this fact with inequalities
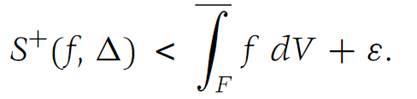
which is the first inequality in part (a) of the theorem.
Theorem 1.1 leads to the following result (stated without proof) on interchanging the order of integration in multiple integrals.
Theorem 1.2
Suppose that F is a domain in RM and that Gx is a domain in RN for each x ∈ F. Define B ={(x, y): x ∈ F, y ∈ Gx for each such x}. Let f :B → R1 be integrable over B and suppose that f is integrable over Gx for each x ∈ F.
Then the function
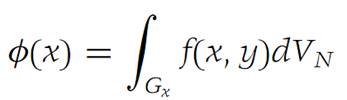
is integrable over F, and
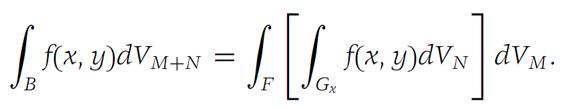
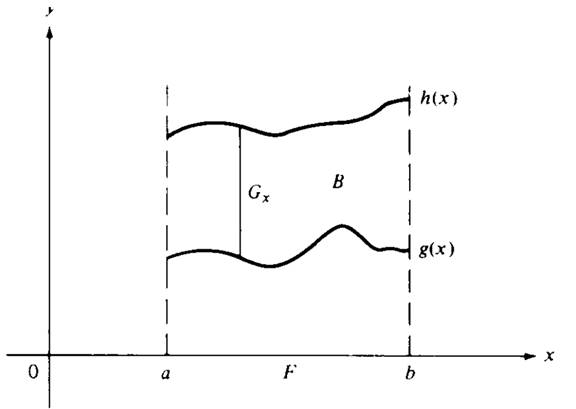
Figure 1.1 B ={(x, y) : a ≤ x ≤ b, y ∈ Gx}.
Figure 1.1 shows a simple illustration of the theorem for functions on R2. Let B ={(x, y) : a ≤ x ≤ b, g(x) ≤ y ≤ h(x)}. Then F ={x : a ≤ x ≤ b} and Gx ={y : g(x) ≤ y ≤ h(x) for each x}. The theorem states that
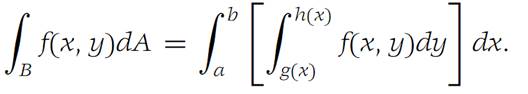
Problems
1. Prove that the Riemann integral of a function in RN is unique.
2. Suppose that F is a domain in RN for N ≥ 2 and that f : F → R1 is Riemann integrable on F. Show that f need not be bounded on F.
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(145-149)



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|