The development of the theory of integration in R^N for N ≥ 2 parallels the one-dimensional case given in Section of (The Darboux Integral for Functions on R¹). For functions defined on an interval I in R¹, we formed upper and lower sums by dividing I into a number of subintervals. In R^N we begin with a domain F, i.e., a bounded region that has volume, and in order to form upper and lower sums, we divide F into a number of subdomains. These subdomains are the generalizations of the subinterval in R¹, and the limits of the upper and lower sums as the number of subdomainstends to infinity yield upper and lower integrals. The subdomains can be thought of ashypercubesin RN with the volume of each hypercube just N times the length of a side.

Definition

Let F be a bounded set in R^N that is a domain. A subdivision of F is a finite collection of domains {F₁,F₂,...,F_n} no two of which have common interior points and the union of which is F. That is,

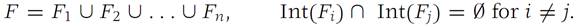
We denote such a subdivision by the single letter Δ.

Let D be a set in R^N containing F and suppose that f : D → R¹ is a bounded function on F. Let  Δ be a subdivision of F and set

Definitions

The upper sum of f with respect to the subdivision  Δ is defined by the formula

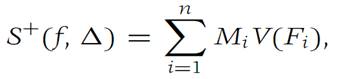
where V(F_i) is the volume in R^N of the domain F_i . Similarly, the lower sum of f is define by

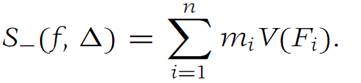
Let  Δ be a subdivision of a domain F. Then  Δ^/, another subdivision of F, is called a refinement of  Δ if every domain of  Δ^/ is entirely contained in one of the domains of  Δ. Suppose that  Δ₁ ={F₁,F₂,...,F_n} and  Δ₂ ={G₁,G₂,...,G_m} are two subdivisions of F. We say that  Δ^/, the subdivision consisting of all nonempty domains of the form F_i ∩ G_j , i = 1, 2,...,n,    j = 1, 2,...,m, is the common refinement of  Δ₁ and  Δ₂. Note that  Δ^/ is a refinement of both  Δ₁ and  Δ₂.

Theorem 1.1

Let F be a domain in R^N and suppose that f :F → R¹ is bounded on F.

(a) If m ≤ f(x) ≤ M for all x ∈ F and if  Δ is any subdivision of F, then

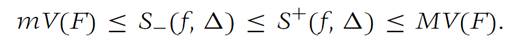
(b) If  Δ^/is a refinement of  Δ, then

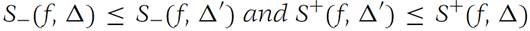
(c) If  Δ₁ and  Δ₂ are any two subdivisions of F, then

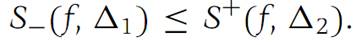
Proof

(a) The proof of part (a) is identical to the proof of part (a) in Theorem1.1 in the (The Darboux Integral for Functions on R^N), the same theorem for functions from R¹ into R¹.

(b) Let  Δ^/={F^/₁,...,F^/_m} be a refinement of  Δ ={F₁,F₂,...,F_n}.We denote by F^/₁,F^/₂,...,F^/_k the domains of  Δ^/ contained in F₁. Then, using the symbols

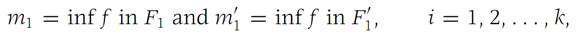
we have immediately m₁ ≤ m^/_i, i =1, 2,...,k, since each F^/_I is a subset of F₁.

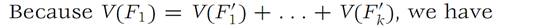
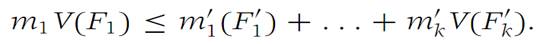
 (1.1)

The same type of inequality as (1.1) holds for F₂,F₃,...,F_n. Summing these inequalities, we get S−(F, Δ) ≤ S−(f, Δ^/). The proof that S+(f, Δ^/) ≤ S+(f, Δ) is similar.

(c) If  Δ₁ and  Δ₂ are two subdivisions, let  Δ^/denote the common refinement. Then, from parts(a) and (b), it follows that  

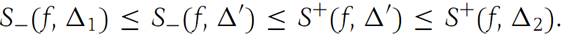
Definitions

Let F be a domain in RN and suppose that f : F → R¹ is bounded on F. The upper integral of f is defined by

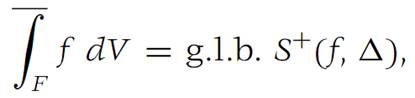
where the greatest lower bound is taken over all subdivisions  Δ of F. The lower integral of f is

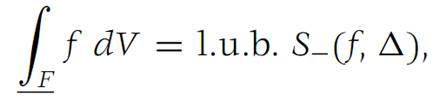
where the least upper bound is taken over all possible subdivisions  Δ of F.If

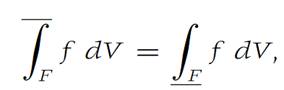
then we say that f is Darboux integrable, or just integrable, on F, and we designate the common value by

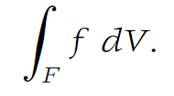
When we wish to emphasize that the integral is N-dimensional, we write

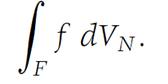
The following elementary results for integrals in R^N are the direct analogues  of the corresponding theorems given in Chapter of(Elementary Theory of Integration)for func- tionsfrom R¹ into R¹. The proofs are the same except for the necessary alterationsfrom intervals in R¹ to domains in Rⁿ.

Theorem 1.2

Let F be a domain in R^N. Let f,f₁,f₂ be functions from F into R¹ that are bounded.

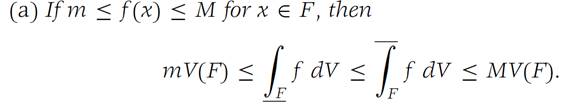
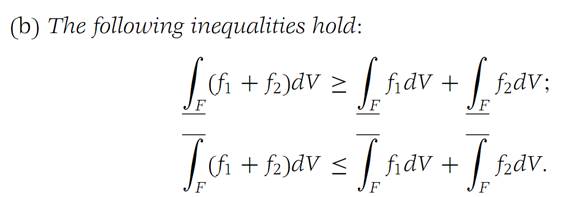
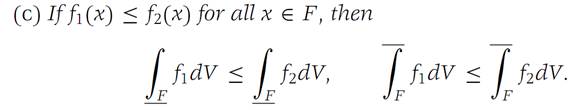
Theorem 1.3

Let F be a domain in R^N and suppose that f :F → R¹ is bounded.

(a) f is Darboux integrable on F if and only if for each ε> 0 there is a subdivision  Δ of F such that

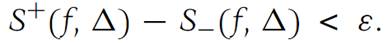
(b) If f is uniformly continuous on F, then F is Darboux integrable on F.

(c) If f is Darboux integrable on F, then |f | is also.

(d) If f₁,f₂ are each Darboux integrable on F, then f₁ · f₂ is also.

(e) If f is Darboux integrable on F, and H is a domain contained in F, then f is Darboux integrable on H.

The proof of Theorem 1.2 follows the lines of the analogous theorem in R1.

For positive functions from an interval I in R¹ to R¹, the Darboux integral gives a formula for finding the area under a curve. If F is a domain in R^N, N ≥ 2, and if f : F → R¹ is a nonnegative function, then the

Darboux integral of  f gives the (N + 1)-dimensional volume “under the hyper surface f .”

Problems

1. Let F be a domain in RN. Give an example of a function f : F → R^N

such that f is bounded on F and

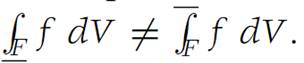
2. Suppose that F is a domain in R^N and that f is integrable over F. Show that

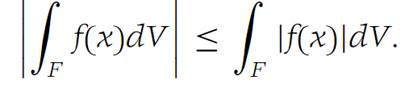
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(140-145)