There are two principal extensions to RN of the theory of differentiation of real-valued functions on R1. In this section, we develop the natural generalization of ordinary differentiation discussed in (Elementary Theory of Differentiation)to partial differentiation of functions from RN to R1. In Section of (The Derivative in RN .), we extend the ordinary derivative to the total derivative. We shall use letters x, y, z, etc. to denote elements in RN. The components of an element x are designated by (x1,x2,...,xN), and as usual, the Euclidean distance, given by the formula

will be used. We also write d(x, y) =|x − y| and d(x, 0) =|x|.
Definition
Let f be a function with domain an open set in RN and range in R1.We define the N functions f ,i with i = 1, 2,...,N by the formulas
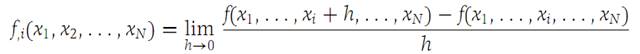
whenever the limit exists. The functions f,1,f,2,...,f,N are called the first partial derivatives of f .
We assume that the reader is familiar with the elementary processes of differentiation. The partial derivative with respect to the ith variable Is computed by holding all other variables constant and calculating the ordinary derivative with respect to xi . That is, to compute f,i at the value a = (a1,a2,...,aN), form the function ϕ (from R1 to R1) by setting
(1.1)
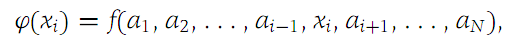
and observe that (1.2)
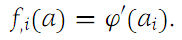
There are many notations for partial differentiation. In addition to the one above, the most common ones are

Good notation is important in studying partial derivatives, since them any letters and subscripts that occur can lead to confusion. The two “best” symbols, especially in discussing partial derivatives of higher order, are f,i and Di f , and we shall employ these most of the time. We recall that the equations of a line segment in RN connecting the points a = (a1,...,aN) and a + h = (a1 + h1,...,aN + hN) are given parametrically by the formulas(the parameter is t)

The next theorem isthe extension to functions from RN to R1 of the Mean-value theorem.
Theorem 1.1 (Extended Mean-value theorem)
Let τi be the line segment in RN connecting the points (a1,a2,...,ai ,...,aN) and (a1,a2,...,ai +hi ,...,aN). Suppose f is a function from RN into R1 with domain containing τi , and suppose that the domain of f,i contains τi . Then there is a real number ξi on the closed interval in R1 with endpoints ai and ai + hi such that (1.3)

Proof
If hi = 0, then equation (1.3) holds. If hi = 0, we use the notation of expression (1.1) to write the left side of equation (1.3) in the form

For this function on R , we apply the Mean-value theorem to conclude that

This formula is a restatement of equation (1.3). (Theorem of(Fundamental lemma of differentiation) Suppose that f has a derivative at x0. Then there is a function η defined in aninterval about 0 such that f(x0 + h) − f(x0) = [f/(x0) + η(h)] · h. Also, η is continuous at 0 with η(0) = 0.)),
the Fundamental lemma of differentiation, has the following generalization for functions from RN into R1.We state the theorem in the general case and prove it for N= 2.
Theorem 1.2 (Fundamental lemma of differentiation)
Suppose that the functions f and f,1,f,2,...,f,N all have a domain in RN that contains an open ball about the point a = (a1,a2,...,aN). Suppose all the f,I i = 1,2,...,N, are continuous at a. Then
(a) f is continuous at a;
(b) there are functions Ԑ1(x), Ԑ2(x),...,ԐN(x), continuous at x= 0, such
that Ԑ1(0) =Ԑ2(0) = ... = ԐN(0) = 0 and(1.4)

for h = (h1,h2,...,hN) in some ball B(0,r) in RN of radius r and center at h = 0.
Proof
For N =2. We employ the identity (1.5)

Since f, f,1, and f,2 are defined in an open ball about a =(a1,a2), this identity is valid for h1,h2 in a sufficiently small ball (of radius, say, r) about h1 = h2 = 0. Applying Theorem 1.1 to the right side of equation (1.5), we find that there are numbers ξ1(h1,h2), ξ2(h1,h2) on the closed intervals from a1 to a1 + h1 and from a2 to a2 + h2, respectively, such that (1.6)

Equation (1.6) is valid for h1,h2 in the ball of radius r about h1 = h2 = 0.
Now define(1.7)

We wish to show that Ԑ1 and Ԑ2 are continuous at (0, 0). Let Ԑ> 0 be given
Since f,1 and f= are continuous at (a1,a2), there is a δ> 0 such that)1.8)
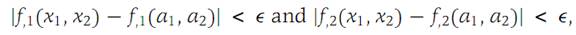
for (x1,x2) in a ball of radius δ with center at (a1,a2). Comparing expressions (1.7) and (1.8), we see that if h1 and h2 are sufficiently small (so that (ξ1,ξ2) is close to (a1,a2)), then
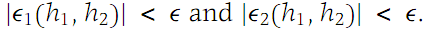
Moreover, Ԑ1(0, 0) =0 and Ԑ2(0, 0) =0. Substituting the values of Ԑ1 and Ԑ2 from equations (1.7) into equation (1.6) we obtain part (b) of the theorem. The continuity of f at (a1,a2) follows directly from Equation (1.4).
The proof for N> 2 is similar.
The chain rule for ordinary differentiation can be extended to provide a rule for taking partial derivatives of composite functions. We establish the result for a function f : RN → R1 when it is composed with N functions g1,g2,...,gN each of which is a mapping from RM into R1. The integer M may be different from N. If Y= (y1,y2,...,yN) and x =(x1,x2,...,xM) are elements of RN and RM, respectively, then in customary terms, we wish to calculate the derivative of H(x) (a function from RM into R1) with respect to xj , where f= f(y1,y2,...,yN) and
(1.9) H(x) =f [g1(x), g2(x),...,gN(x)].
Theorem 1.3 (Chain rule)
Suppose that each of the functions g1,g2,...,gN is amapping from RM into R1.
For a fixed integer j between 1 and M, assume that g1,j,g2,j,...,gN,j are defined at some point b = (b1,b2,...,bM). Suppose that f and its partial derivatives f,1,f,2,...,f,N are continuous at the point a = (g1(b),g2(b),...,gN(b)). Form the function H as in equation (1.9). Then the partial derivative of H with respect to xj isgiven by

Proof
Define the following functions from R1 into R1.
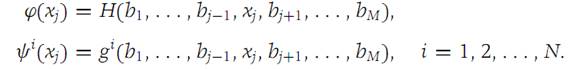
Then, according to equation (1.9), we have
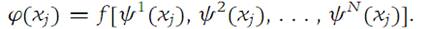
With h denoting a real number, define
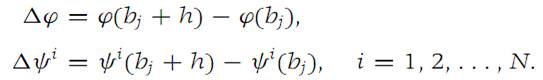
Since each ψi is continuous at bj , it follows that Δψi → 0as h → 0. We apply equation (1.4) from Theorem 1.2 to the function ϕ and use Δψi instead of hi in that equation. We obtain(1.10)

In this formula, we have Ԑi= Ԑi(Δψ1,...,ΔψN) and Ԑi → 0as Δψk → 0, K= 1, 2,...,N.
Now write equation (1.10) in the form
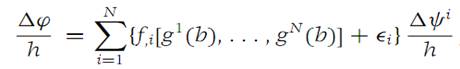
valid for |h| sufficiently small. Letting h tend to 0, we get the statement of the Chain rule.
Problems
1. Let D be a ball in RN and suppose f : D → R1 has the property that f,1 = f,2 =···= f,N = 0 for all x ∈ D. Show that f ≡ constant in D.
2. Let f : RN → R1 be given and suppose that g1,g2,...,gN are N functions from RM into R1. Let h1,h2,...,hM be M functions from Rp into R1. Give a formula for the Chain rule for H,i(x), where
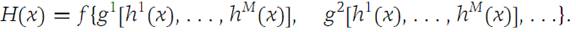
3. Write a proof of Theorem 1.2for N =3.
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(125-129)
 الاكثر قراءة في التحليل الحقيقي
الاكثر قراءة في التحليل الحقيقي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


