


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-11-2016
Date: 22-11-2016
Date: 23-11-2016
|
In this section we establish a theorem that is useful in the further development of differentiation and integration. The Heine–Borel theorem shows that “covering” a set with a collection of special sets is particularly helpful in verifying uniform continuity. Consider, for example, the collection of intervals(1.9)
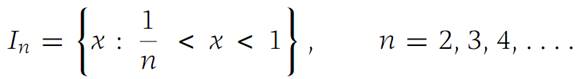
Any collection of intervals such as(1.9) is called a family of intervals. The symbol F is usually used to denote the totality of intervals in the family. Each interval is called a member (or element) of the family. Care must be exercised to distinguish the points of a particular interval from the interval itself. In the above example, the interval J ={x :1/3 <x< 2/3 } is not a member of F. However, every point of J is in every interval In for n> 2. The points0 <x< 1 are not themselves members of F although each point of 0 <x< 1 is in at least one In.
Definitions
A family F of intervals is said to cover the set S in R1 if each point of S is in at least one of the intervals of F. A family F1 is a subfamily of F if each member of F1 is a member of F.
For example, the intervals(1.10)
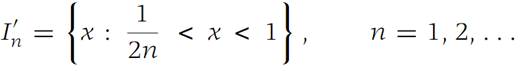
form a subfamily of family (1.9). Family (1.9) covers the set S ={x :0 < x< 1}, since every number x such that 0 <x< 1isin In for all n larger than 1/x. Thus every x is in at least one In. Family (1.10) also covers S.
More generally, we may consider a collection of sets A1,A2 ...An,..., which we call a family of sets. We use the same symbol F to denote such a family. A family F covers a set S if and only if every point of S is a point in at least one member of F. The family F,
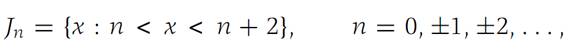
Covers all of R1. It is simple to verify that if any interval is removed from F, the resulting family fails to cover R1. For example, if J1 is removed, then no member of the remaining intervals of F contains the number 2.
We shall be interested in families of open intervals that contain infinitely many members and that cover a set S. We shall examine those sets S that have the property that they are covered by a finite subfamily, i.e., a subfamily with only a finite number of members. For example, the family F of intervals Kn ={x :1/(n + 2)<x< 1/n}, n = 1, 2,...,
Covers the set S {x :0 <x< 1/2 }, as is easily verified. It may also be verified that no finite subfamily of F ={Kn} covers S. However, if we consider the set S1 ={x : ε<x< 1 2 } for any ε> 0, it is clear that S1 is covered by the finite subfamily {K1,K2,...,Kn} for any n such that n + 2 > 1/ε.
We may define families of interval sindirectly. For example, suppose that f : x → 1/x with domain D ={x :0 <x ≤ 1} is given. We obtain a family F of intervals by considering all solution sets of the inequality(1.11)
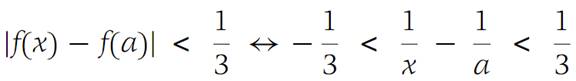
for every a ∈ D. For each value a, the interval(1.12)
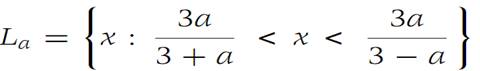
Is the solution of Inequality (1.11). This family F ={La} covers the set D ={x :0 <x ≤ 1}, but no finite subfamily covers D.
Theorem 1.1 (Heine–Borel theorem)
Suppose that a family F of open intervals covers the closed interval I ={x:a ≤ x ≤ b}. Then a finite subfamily of F covers I.
Proof
We shall suppose that an infinite number of members of F are required to cover I and reach a contradiction. Divide I into two equal parts at the midpoint. Then an infinite number of members of F are required to cover either the left subinterval or the right subinterval of I. Denote by I1 ={x : a1 ≤ x ≤ b1} the particular subinterval needing this infinity of members of F. We proceed by dividing I1 into two equal parts, and denote by I2 ={x : a2 ≤ x ≤ b2} that half of I1 that requires an infinite number of members of F. Repeating the argument, we obtain a sequence of closed intervals In ={x : an ≤ x ≤ bn}, n = 1, 2,..., each of which requires an infinite number of intervals of F in order to be covered. Since bn − an= (b − a)/2n → 0as n →∞, the Nested intervals theorem states that there is a unique number x0 ∈ I that is in every In. However, since F covers I, there is a member of F, say J ={x : α<x<β}, such that x0 ∈ J . By choosing N sufficiently large, we can find an IN contained in J . But this contradicts the fact that infinitely many intervals of F are required to cover IN, since we found that the one interval J covers IN.
In the Heine–Borel theorem, the hypothesis that I ={x : a ≤ x ≤ b} Is a closed interval iscrucial. The open interval J1 ={x :0 <x< 1} is covered by the family F of intervals(1.9), but no finite subfamily of F covers J1.
Problems
In each of Problems 1 through 6 decide whether or not the infinite sequence is a Cauchy sequence. If it is not a Cauchy sequence, find at least one subsequence that is a Cauchy sequence. In each case n = 1, 2,....
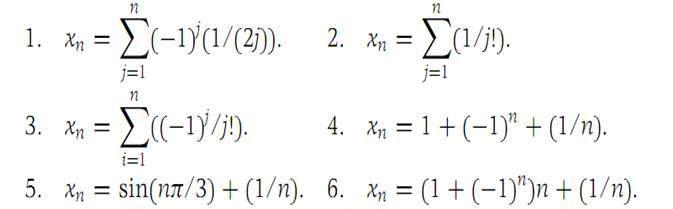
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(63-65)



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|