Each partial derivative of a function f : R^N → R¹ isa mapping from R^N into R¹. This generalization of the ordinary derivative, useful for many purposes, singles out a particular direction in which the differentiation is performed. We now take up another extension of the ordinary derivative, one in which the difference quotient tends to a limit as x → a regardless of the direction of approach.

Let A be an open subset of R^N, and suppose that f and g are functions from A into R¹. We denote by d(x, y) the Euclidean distance between two points x, y in R^N.

Definition

The continuous functions f and g are tangent at a point a ∈ A if

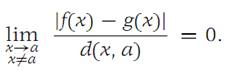
We note that if two functions are tangent at a point a, then necessarily f(a) = g(a). Also, if f , g, and h are functions with f and g tangent at a and with g and h tangent at a, then we verify simply that f and h are tangent at a. To see this, observe that

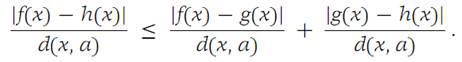
As x → a, the right side tends to 0, and so must the left side.

Let L : R^N → R¹ be a linear function; that is, L is of the form                                           

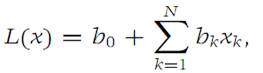
where b₀,b₁,...,b_N are real numbers. It may happen that a function f is tangent to a linear function at a point a. If so, this linear function is unique, as we now show.

Theorem 1.1

Suppose that L₁ and L₂ are linear functions tangent to a function f at a point a. Then L₁ ≡ L₂.

Proof

It is convenient to write the linear functions L₁ and L₂ in the form

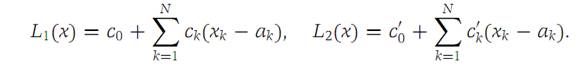
From the discussion above, it follows that L₁(a) = L₂(a) = f(a). Hence, c₀ = c^/0. Also, for every Ԑ> 0, we have(1.1)

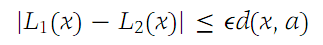
for all x sufficiently close to a. For z ∈ R^N, we use the notation z=d(z, 0). Now, with δ a real number, choose

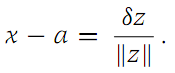
Then, for sufficiently small |δ|, we find from inequality (1.1) that

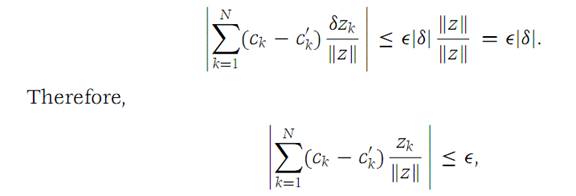
and since this inequality holds for all positive Ԑ, we must have c_k = c^/_k, k =1, 2,...,N.

Definitions

Suppose that f : A → R¹ is given ,where A is an open set in R^N containing the point a. The function f is differentiable at a if there is a linear function

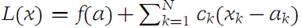
that is tangent to f at a. A function  f is differentiable on a set A in R^N if it is differentiable at each point of A. The function L is called the derivative, or total derivative, of at . We use the symbol f^/(a) for the derivative of  f at the point a in R^N.

Theorem 1.2

If f is differentiable at a point a, then f is continuous at a. The proof is left to the reader. (Problem3 at the end of this section.) As we saw in Section of (Partial Derivatives and the Chain Rule (, a function f may have partial derivatives without being continuous. suggests that differentiability is a stronger condition than the existence of partial derivatives. The next theorem verifies this point.

Theorem 1.3

If f is differentiable at a point a, then all first partial derivatives of f exist at a.

Proof

Let L be the total derivative of f at a. We write

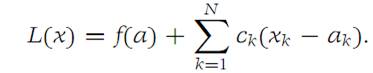
From the definition of derivative, it follows that(1.2)

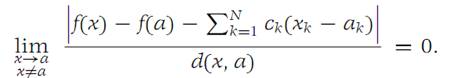
For x we choose the element a + h, where h = (0, 0,..., 0,h_i , 0,..., 0). Then equation (1.2) becomes

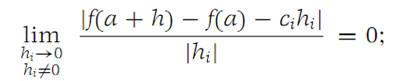
we may therefore write(1.3)

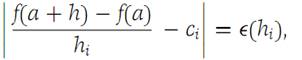
where Ԑ(h_i) → 0as h_i → 0.

We recognize the left side of equation (1.3) as the expression used in the definition of f,i(a). In fact, we conclude that

                                                                      c_i =f_,i(a), i = 1, 2,...,N.

A partial converse of Theorem1.3 is also true.

Theorem 1.4

Suppose that f_,i , i = 1,2,...,N, are continuous at a point a. Then f is differentiable at a. This result is most easily established by means of the Taylor expansion with remainder with n= 0. We leave the details for the reader.

Definitions

Suppose that f possesses all first partial derivatives at a point a in R^N. The gradient of f is the element in R^N whose components are (f_,1(a), f_,2(a),...,f_,N(a)). We denote the gradient of f by ∇f or grad f .

Suppose that A is a subset of R^N and f : A → R¹ is differentiable on A. Let h =(h₁,h₂,...,h_N) be an element of R^N. We define the total differential df as that function from A × R^N → R¹ given by the formula(1.4)

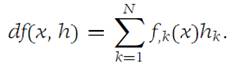
Using the inner or dot product notation for elements in RN, we may also write

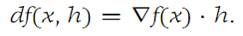
Equation (1.4) shows that the total differential (also called the dif ferential) of a function f is linear in h. The differential vanishes when x =a and h= 0. The Chain rule takes a natural form for differentiable functions, as the following theorem shows.

Theorem 1.5 (Chain rule)

Suppose that each of the functions g¹,g²,...,g^N is a mapping from R^M into R¹ and that each gⁱ is differentiable at a point b= (b₁,b₂,...,b_M). Suppose that f :R^N → R¹ is differentiable at the point a = (g₁(b),g₂(b),...,g_N(b)).

Form the function

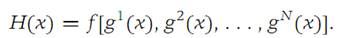
Then H is differentiable at b and

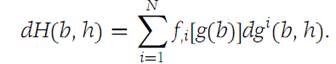
Problems

1. Let f and g be functions from R^N into R¹. Show that if f and g are differentiable at a point a, then f + g is differentiable at a. Also, αf is differentiable at a for every real number α.

2. Let f : R³ → R¹ be given by

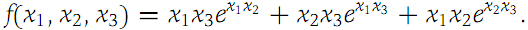
Find ∇f and df(x, h).

3. Suppose that all first partial derivatives of a function f : R^N → R¹ are continuous at a point a. Show that f is differentiable at a.(Theorem 1.4.)

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(136-140)