


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-5-2021
Date: 13-5-2021
Date: 29-7-2021
|
Let X be a topological space, and let A be a subset of X. A collection of subsets of X in X is said to cover A if and only if every point of A belongs to at least one of these subsets. In particular, an open cover of X is collection of open sets in X that covers X.
If U and V are open covers of some topological space X then V is said to be a subcover of U if and only if every open set belonging to V also belongs to U.
Definition: A topological space X is said to be compact if and only if every open cover of X possesses a finite subcover.
Lemma 1.1 Let X be a topological space. A subset A of X is compact (with respect to the subspace topology on A) if and only if, given any collection U of open sets in X covering A, there exists a finite collection V1, V2, . . . , Vr of open sets belonging to U such that A ⊂ V1 ∪ V2 ∪ · · · ∪ Vr.
Proof A subset B of A is open in A (with respect to the subspace topology on A) if and only if B = A ∩V for some open set V in X. The desired result therefore follows directly from the definition of compactness.
We now show that any closed bounded interval in the real line is compact.
This result is known as the Heine-Borel Theorem. The proof of this theorem uses the least upper bound principle which states that, given any non-empty set S of real numbers which is bounded above, there exists a least upper bound (or supremum) sup S for the set S.
Theorem 1.2 (Heine-Borel) Let a and b be real numbers satisfying a < b.
Then the closed bounded interval [a, b] is a compact subset of R.
Proof Let U be a collection of open sets in R with the property that each point of the interval [a, b] belongs to at least one of these open sets. We must show that [a, b] is covered by finitely many of these open sets.
Let S be the set of all τ ∈ [a, b] with the property that [a, τ ] is covered by some finite collection of open sets belonging to U, and let s = sup S. Now s ∈ W for some open set W belonging to U. Moreover W is open in R, and therefore there exists some δ > 0 such that (s − δ, s + δ) ⊂ W. Moreover s − δ is not an upper bound for the set S, hence there exists some τ ∈ S satisfying τ > s − δ. It follows from the definition of S that [a, τ ] is covered by some finite collection V1, V2, . . . , Vr of open sets belonging to U.
Let t ∈ [a, b] satisfy τ ≤ t < s + δ. Then
[a, t] ⊂ [a, τ ] ∪ (s − δ, s + δ) ⊂ V1 ∪ V2 ∪ · · · ∪ Vr ∪ W,
and thus t ∈ S. In particular s ∈ S, and moreover s = b, since otherwise s would not be an upper bound of the set S. Thus b ∈ S, and therefore [a, b] is covered by a finite collection of open sets belonging to U, as required.
Lemma 1.3 Let A be a closed subset of some compact topological space X.
Then A is compact.
Proof Let U be any collection of open sets in X covering A. On adjoining the open set X A to U, we obtain an open cover of X. This open cover of X possesses a finite subcover, since X is compact. Moreover A is covered by the open sets in the collection U that belong to this finite subcover. It follows from Lemma 1.11 that A is compact, as required.
Lemma 1.4 Let f: X → Y be a continuous function between topological spaces X and Y , and let A be a compact subset of X. Then f(A) is a compact subset of Y .
Proof Let V be a collection of open sets in Y which covers f(A). Then A is covered by the collection of all open sets of the form f−1 (V ) for some V ∈ V.
It follows from the compactness of A that there exists a finite collection V1, V2, . . . , Vk of open sets belonging to V such that A ⊂ f−1 (V1) ∪ f−1 (V2) ∪ · · · ∪ f−1 (Vk).
But then f(A) ⊂ V1 ∪ V2 ∪ · · · ∪ Vk. This shows that f(A) is compact.
Lemma 1.5 Let f:X → R be a continuous real-valued function on a compact topological space X. Then f is bounded above and below on X.
Proof The range f(X) of the function f is covered by some finite collection I1, I2, . . . , Ik of open intervals of the form (−m, m), where m ∈ N, since f(X) is compact (Lemma 1.14) and R is covered by the collection of all intervals of this form. It follows that f(X) ⊂ (−M, M), where (−M, M) is the largest of the intervals I1, I2, . . . , Ik. Thus the function f is bounded above and below on X, as required.
Proposition 1.6 Let f: X → R be a continuous real-valued function on a compact topological space X. Then there exist points u and v of X such that f(u) ≤ f(x) ≤ f(v) for all x ∈ X.
Proof Let m = inf{f(x) : x ∈ X} and M = sup{f(x) : x ∈ X}. There must exist v ∈ X satisfying f(v) = M, for if f(x) < M for all x ∈ X then the function x → 1/(M − f(x)) would be a continuous real-valued function on X that was not bounded above, contradicting Lemma 1.15. Similarly there must exist u ∈ X satisfying f(u) = m, since otherwise the function x → 1/(f(x)−m) would be a continuous function on X that was not bounded above, again contradicting Lemma 1.15. But then f(u) ≤ f(x) ≤ f(v) for all x ∈ X, as required.
Proposition 1.7 Let A be a compact subset of a metric space X. Then A is closed in X.
Proof Let p be a point of X that does not belong to A, and let f(x) = d(x,p), where d is the distance function on X. It follows from Proposition 1.16 that there is a point q of A such that f(a) ≥ f(q) for all a ∈ A, since A is compact. Now f(q) > 0, since q ≠p. Let δ satisfy 0 < δ ≤ f(q).
Then the open ball of radius about the point p is contained in the complement of δ, since f(x) < f(q) for all points x of this open ball. It follows that the complement of A is an open set in X, and thus A itself is closed in X.
Proposition 1.8 Let X be a Hausdorff topological space, and let K be a compact subset of X. Let x be a point of X K. Then there exist open sets V and W in X such that x ∈ V , K ⊂ W and V ∩ W = ∅.
Proof For each point y ∈ K there exist open sets Vx,y and Wx,y such that x ∈ Vx,y, y ∈ Wx,y and Vx,y ∩ Wx,y = ∅ (since X is a Hausdorff space). But then there exists a finite set {y1, y2, . . . , yr} of points of K such that K is contained in Wx,y1 ∪ Wx,y2 ∪ · · · ∪ Wx,yr, since K is compact. Define
V = Vx,y1 ∩ Vx,y2 ∩ · · · ∩ Vx,yr , W = Wx,y1 ∪ Wx,y2 ∪ · · · ∪ Wx,yr.
Then V and W are open sets, x ∈ V , K ⊂ W and V ∩W = ∅, as required.
Corollary 1.9 A compact subset of a Hausdorff topological space is closed.
Proof Let K be a compact subset of a Hausdorff topological space X. It follows immediately from Proposition 1.18 that, for each x ∈ X K, there exists an open set Vx such that x ∈ Vx and Vx ∩ K = ∅. But then X K is equal to the union of the open sets Vx as x ranges over all points of X K, and any set that is a union of open sets is itself an open set. We conclude that X K is open, and thus K is closed.
Proposition 1.10 Let X be a Hausdorff topological space, and let K1 and K2 be compact subsets of X, where K1 ∩ K2 = ∅. Then there exist open sets U1 and U2 such that K1 ⊂ U1, K2 ⊂ U2 and U1 ∩ U2 = ∅.
Proof It follows from Proposition 1.18 that, for each point x of K1, there exist open sets Vx and Wx such that x ∈ Vx, K2 ⊂ Wx and Vx ∩Wx = ∅. But then there exists a finite set {x1, x2, . . . , xr} of points of K1 such that
K1 ⊂ Vx1 ∪ Vx2 ∪ · · · ∪ Vxr,
since K1 is compact. DefineU1 = Vx1 ∪ Vx2 ∪ · · · ∪ Vxr, U2 = Wx1 ∩ Wx2 ∩ · · · ∩ Wxr.
Then U1 and U2 are open sets, K1 ⊂ U1, K2 ⊂ U2 and U1 ∩ U2 = ∅, as required.
Lemma 1.11 Let f:X → Y be a continuous function from a compact topological space X to a Hausdorff space Y . Then f(K) is closed in Y for every closed set K in X.
Proof If K is a closed set in X, then K is compact (Lemma 1.13), and therefore f(K) is compact (Lemma 1.14). But any compact subset of a Hausdorff space is closed (Corollary 1.19). Thus f(K) is closed in Y , as required.
Remark : If the Hausdorff space Y in Lemma 1.21 is a metric space, then Proposition 1.17 may be used in place of Corollary 1.12 in the proof of the lemma.
Theorem 1.13 A continuous bijection f: X → Y from a compact topological space X to a Hausdorff space Y is a homeomorphism.
Proof Let g: Y → X be the inverse of the bijection f: X → Y . If U is open in X then X U is closed in X, and hence f(X U) is closed in Y , by Lemma 1.21. But f(X U) = g−1 (X U) = Y g−1 (U). It follows that g−1 (U) is open in Y for every open set U in X. Therefore g: Y → X is continuous, and thus f: X → Y is a homeomorphism.
We recall that a function f: X → Y from a topological space X to a topological space Y is said to be an identification map if it is surjective and satisfies the following condition: a subset U of Y is open in Y if and only if f−1 (U) is open in X.
Proposition 1.14 A continuous surjection f:X ! Y from a compact topological space X to a Hausdorff space Y is an identication map.
Proof Let U be a subset of Y . We claim that Y U = f(K), where K =X f−1 (U). Clearly f(K) ⊂ Y U. Also, given any y ∈ Y U, there exists x ∈ X satisfying y = f(x), since f: X → Y is surjective. Moreover x ∈ K, since f(x) ∉U. Thus Y U ⊂ f(K), and hence Y U = f(K), as claimed.
We must show that the set U is open in Y if and only if f−1 (U) is open in X. First suppose that f−1 (U) is open in X. Then K is closed in X, andhence f(K) is closed in Y , by Lemma 1.21. It follows that U is open in Y .
Conversely if U is open in Y then f−1 (U) is open in X, since f: X → Y is continuous. Thus the surjection f: X → Y is an identification map.
Example Let S1 be the unit circle in R2, defined by S1 = {(x, y) ∈ R2: x2 + y2 = 1}, and let q: [0, 1] → S1 be defined by q(t) = (cos 2πt,sin 2πt) for all t ∈ [0, 1]. It has been shown that the map q is an identification map. This also follows directly from the fact that q: [0, 1] → S1is a continuoussurjection from the compact space [0, 1] to the Hausdorff space S1.
We shall show that a finite Cartesian product of compact spaces is compact. To prove this, we apply the following result, known as the Tube Lemma.
Lemma 1.15 Let X and Y be topological spaces, let K be a compact subset of Y , and U be an open set in X × Y . Let V = {x ∈ X : {x} × K ⊂ U}.
Then V is an open set in X.
Proof Let x ∈ V . For each y ∈ K there exist open subsets Dy and Ey of X and Y respectively such that (x, y) ∈ Dy × Ey and Dy × Ey ⊂ U.
Now there exists a finite set {y1, y2, . . . , yk} of points of K such that K ⊂ Ey1 ∪ Ey2 ∪ · · · ∪ Eyk, since K is compact. Set Nx = Dy1 ∩ Dy2 ∩ · · · ∩ Dyk.
Then Nx is an open set in X. Moreover
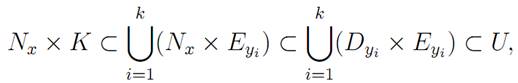
so that Nx ⊂ V . It follows that V is the union of the open sets Nx for all x ∈ V . Thus V is itself an open set in X, as required.
Theorem 1.16 A Cartesian product of a finite number of compact spaces is itself compact.
Proof It suffices to prove that the product of two compact topological spaces X and Y is compact, since the general result then follows easily by induction on the number of compact spaces in the product.
Let U be an open cover of X × Y . We must show that this open cover possesses a finite subcover.
Let x be a point of X. The set {x}×Y is a compact subset of X ×Y , since it is the image of the compact space Y under the continuous map from Y to X × Y which sends y ∈ Y to (x, y), and the image of any compact set under a continuous map is itself compact (Lemma 1.14). Therefore there exists a finite collection U1, U2, . . . , Ur of open sets belonging to the open cover U such that {x} × Y is contained in U1 ∪ U2 ∪ · · · ∪Ur. Let Vx denote the set of all points x0 of X for which {x0} × Y is contained in U1 ∪ U2 ∪ · · · ∪Ur. Then x ∈ Vx, and
Lemma 1.17 ensures That Vx is an open set in X. Note that Vx × Y is covered by finitely many of the open sets belonging to the open cover U.
Now {Vx : x ∈ X} is an open cover of the space X. It follows from the compactness of X that there exists a finite set {x1, x2, . . . , xr} of points of X such that X = Vx1 ∪ Vx2 ∪ · · · ∪ Vxr. Now X × Y is the union of the sets Vxj × Y for j = 1, 2, . . . , r, and each of these sets can be covered by a finite collection of open sets belonging to the open cover U. On combining these finite collections, we obtain a finite collection of open sets belonging to U which covers X × Y . This shows that X × Y is compact.
Theorem 1.18 Let K be a subset of Rn. Then K is compact if and only if K is both closed and bounded.
Proof Suppose that K is compact. Then K is closed, since Rn is Hausdorff, and a compact subset of a Hausdorff space is closed (by Corollary 1.19). For each natural number m, let Bm be the open ball of radius m about the origin, given by Bm = {x ∈ Rn: |x| < m}. Then {Bm : m ∈ N} is an open cover of Rn. It follows from the compactness of K that there exist natural numbers m1, m2, . . . , mk such that K ⊂ Bm1 ∪ Bm2 ∪ · · · ∪ Bmk . But then K ⊂ BM, where M is the maximum of m1, m2, . . . , mk, and thus K is bounded.
Conversely suppose that K is both closed and bounded. Then there exists some real number L such that K is contained within the closed cube C given by
C = {(x1, x2, . . . , xn) ∈ Rn : −L ≤ xj ≤ L for j = 1, 2, . . . , n}.
Now the closed interval [ L, L] is compact by the Heine-Borel Theorem (Theorem 1.12), and C is the Cartesian product of n copies of the compact set [ L,L]. It follows from Theorem 1.25 that C is compact. But K is a closed subset of C, and a closed subset of a compact topological space is itself compact, by Lemma 1.13. Thus K is compact, as required.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|