Betti numbers are topological objects which were proved to be invariants by Poincaré, and used by him to extend the polyhedral formula to higher dimensional spaces. Informally, the Betti number is the maximum number of cuts that can be made without dividing a surface into two separate pieces (Gardner 1984, pp. 9-10). Formally, the 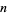th Betti number is the rank of the 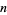th homology group of a topological space. The following table gives the Betti number of some common surfaces.

Let 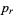 be the group rank of the homology group  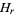of a topological space 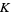. For a closed, orientable surface of genus 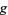, the Betti numbers are 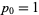, , 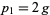and 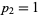. For a nonorientable surface with  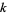cross-caps, the Betti numbers are 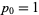, , 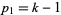and .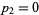

The Betti number of a finitely generated Abelian group 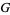 is the (uniquely determined) number  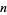such that

where 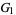, ...,  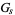are finite cyclic groups (see Kronecker decomposition theorem).

The Betti numbers of a finitely generated module 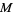 over a commutative Noetherian local unit ring  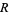are the minimal numbers  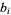for which there exists a long exact sequence

which is called a minimal free resolution of 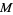. The Betti numbers are uniquely determined by requiring that  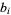be the minimal number of generators of  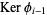for all 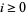. These Betti numbers are defined in the same way for finitely generated positively graded 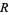-modules if  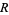is a polynomial ring over a field.

REFERENCES:

Bruns, W. and Herzog, J. Cohen-Macaulay Rings, 2nd ed. Cambridge, England: Cambridge University Press, 1998.

Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 9-11 and 15-16, 1984.

Munkres, J. R. Elements of Algebraic Topology. New York: Perseus Books Pub.,p. 24, 1993.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد