

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Thurston,s Geometrization Conjecture
المؤلف:
Anderson, M. T.
المصدر:
"Scalar Curvature and Geometrization Conjectures for 3-Manifolds." MSRI Publ. 30, 1997. https://www.math.sunysb.edu/~anderson/.
الجزء والصفحة:
...
15-8-2021
5587
Thurston's Geometrization Conjecture
Thurston's conjecture proposed a complete characterization of geometric structures on three-dimensional manifolds.
Before stating Thurston's geometrization conjecture in detail, some background information is useful. Three-dimensional manifolds possess what is known as a standard two-level decomposition. First, there is the connected sum decomposition, which says that every compact three-manifold is the connected sum of a unique collection of prime three-manifolds.
The second decomposition is the Jaco-Shalen-Johannson torus decomposition, which states that irreducible orientable compact 3-manifolds have a canonical (up to isotopy) minimal collection of disjointly embedded incompressible tori such that each component of the 3-manifold removed by the tori is either "atoroidal" or "Seifert-fibered."
Thurston's conjecture is that, after you split a three-manifold into its connected sum and the Jaco-Shalen-Johannson torus decomposition, the remaining components each admit exactly one of the following geometries:
1. Euclidean geometry,
2. Hyperbolic geometry,
3. Spherical geometry,
4. The geometry of 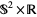 ,
,
5. The geometry of 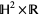 ,
,
6. The geometry of the universal cover 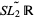 of the Lie group
of the Lie group 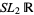 ,
,
7. Nil geometry, or
8. Sol geometry.
Here, 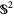 is the 2-sphere (in a topologist's sense) and
is the 2-sphere (in a topologist's sense) and 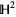 is the hyperbolic plane. If Thurston's conjecture is true, the truth of the Poincaré conjecture immediately follows. Thurston shared the 1982 Fields Medal for work done in proving that the conjecture held in a subset of these cases.
is the hyperbolic plane. If Thurston's conjecture is true, the truth of the Poincaré conjecture immediately follows. Thurston shared the 1982 Fields Medal for work done in proving that the conjecture held in a subset of these cases.
Six of these geometries are now well understood, and there has been a great deal of progress with hyperbolic geometry (the geometry of constant negative scalar curvature). However, the geometry of constant positive curvature is still poorly understood, and in this geometry, the Thurston elliptization conjecture extends the Poincaré conjecture (Milnor).
Results due to Perelman (2002, 2003) appear to establish the geometrization conjecture, and thus also the Poincaré conjecture. Unlike a number of previous manuscripts attempting to prove the Poincaré conjecture, mathematicians familiar with Perelman's work describe it as well thought-out and expect that it will be difficult to locate any mistakes (Robinson 2003).
REFERENCES:
Anderson, M. T. "Scalar Curvature and Geometrization Conjectures for 3-Manifolds." MSRI Publ. 30, 1997. https://www.math.sunysb.edu/~anderson/.
Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.
Milnor, J. "The Poincaré Conjecture." https://www.claymath.org/millennium/Poincare_Conjecture/Official_Problem_Description.pdf.
Milnor, J. Collected Papers, Vol. 2: The Fundamental Group. Publish or Perish Press, p. 93, 1995.
Perelman, G. "The Entropy Formula for the Ricci Flow and Its Geometric Application" 11 Nov 2002. https://arxiv.org/abs/math.DG/0211159.
Perelman, G. "Ricci Flow with Surgery on Three-Manifolds" 10 Mar 2003. https://arxiv.org/abs/math.DG/0303109.
Robinson, S. "Russian Reports He Has Solved a Celebrated Math Problem." The New York Times, p. D3, April 15, 2003.
Thurston, W. P. "Three-Dimensional Manifolds, Kleinian Groups and Hyperbolic Geometry." Bull. Amer. Math. Soc. 6, 357-381, 1982.
Weisstein, E. W. "Poincaré Conjecture Proved--This Time for Real." MathWorld Headline News, Apr. 15, 2003. https://mathworld.wolfram.com/news/2003-04-15/poincare/.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















