


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 11-8-2016
Date: 1-8-2016
Date: 2-8-2016
|
Otto Cycle
The cycle of a highly idealized gasoline engine can be approximated by the Otto cycle (see Figure 1.1).1→2 and 3→4 are adiabatic compression and expansion, respectively; 2→3 and 4→1 are constant-volume processes. Treat the working medium as an ideal gas with constant γ = cp/cv.

Figure 1.1
a) Compute the efficiency of this cycle for γ = 1.4 and compression ratio r = Vi/Vf = 10.
b) Calculate the work done on the gas in the compression process 1→2, assuming initial volume Vi = 2L and Pi = 1 atm.
SOLUTION
a) The efficiency of the cycle is η = W/Q1, where W is the work done by the cycle Q1 and is the amount of heat absorbed by the gas. Because the working medium returns to its initial state W = Q1 – Q2, where Q2 is the amount of heat transferred from the gas, therefore
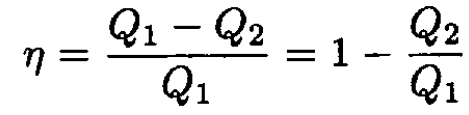 (1)
(1)
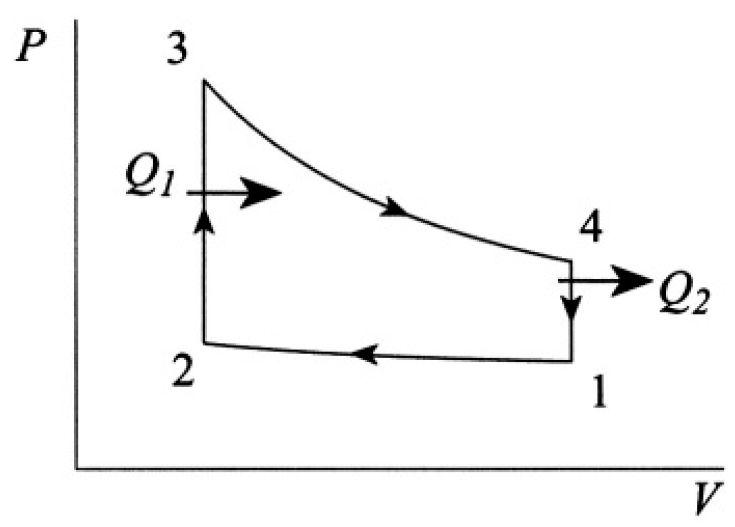
Figure 1.2
Let us calculate Q1 and Q2. Since both processes are at constant volume (see Figure 1.2), we may write
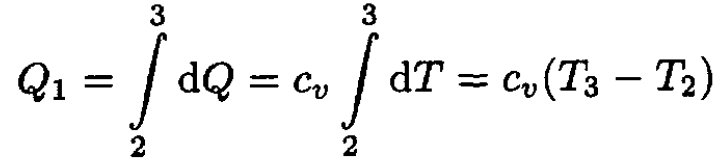 (2)
(2)
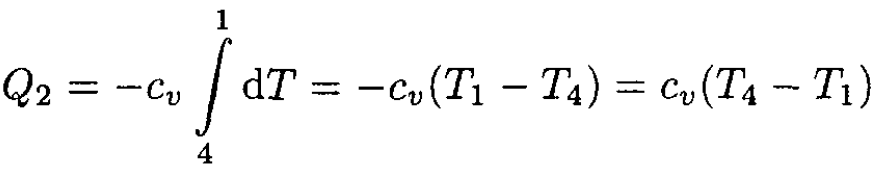
and
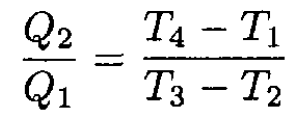 (3)
(3)
We know that for an adiabatic process
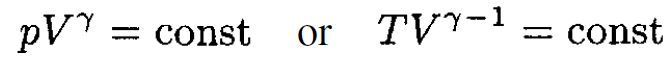
So
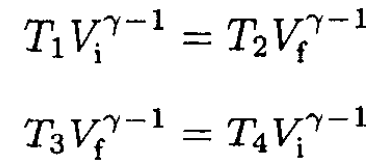 (4)
(4)
Using
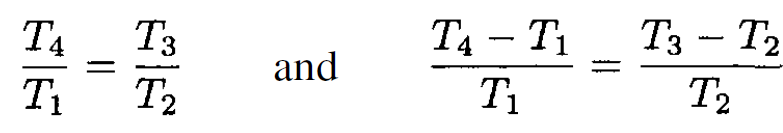 (5)
(5)
we find
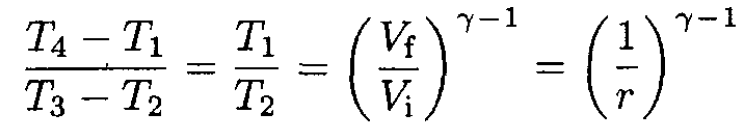 (6)
(6)
and therefore the efficiency is
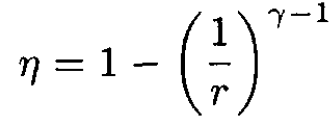 (6)
(6)
For γ = 1.4 and r = 10 the efficiency is
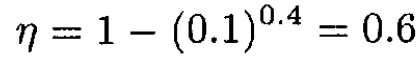 (7)
(7)
b) The work done on the gas in the compression process is
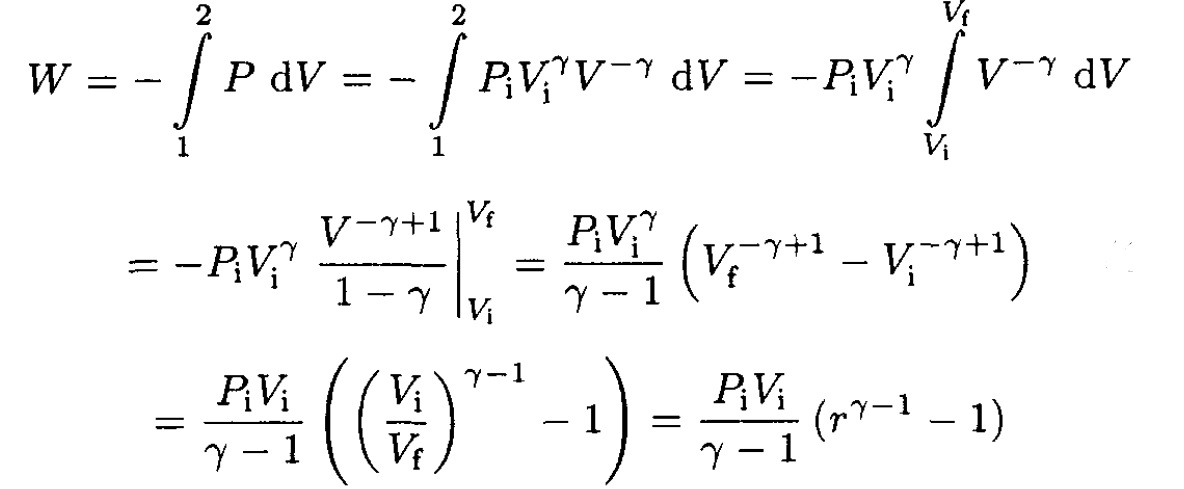 (8)
(8)
For Vi = 2 L and Pi = 1 atm,
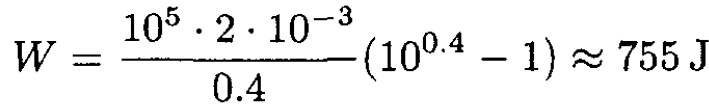



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل: شراكتنا مع المؤسّسات الرائدة تفتح آفاقًا جديدة للارتقاء بجودة التعليم الطبّي في العراق
|
|
|