


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 9-8-2016
Date: 14-8-2016
Date: 30-8-2016
|
Six Uniform Rods
Six equal uniform rods, fastened at their ends by frictionless pivots, form a regular hexagon and lie on a frictionless surface. A blow is given at a right angle to the midpoint of one of them at point P in Figure 1.1 so that it begins to slide with velocity u. Show that the opposite rod begins to move with velocity v = u /10.
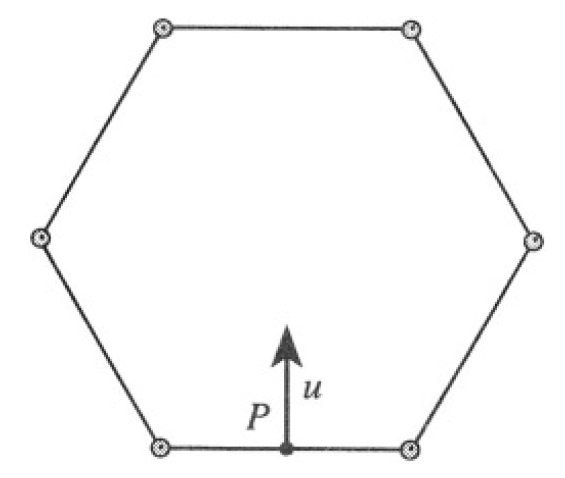
Figure 1.1
SOLUTION
This problem, in general (after some arbitrary time t) is rather difficult. However we can use two important simplifications at t = 0. First, there is six fold symmetry, which means that the positions of the center of mass of each rod can be described by just one angle θ and, of course, the length of a rod, which we will denote as 2a. The other consideration is that even after the blow, the system will keep symmetry relative to the y-axis (because the blow is at midpoint of the first rod). That means that not only at t = 0, but also at later times, there will be no rotation of the system, and its angular momentum is zero. We choose the coordinate system as shown in Figure 1.2. Now the velocity of the center of mass (midpoint P) of the first
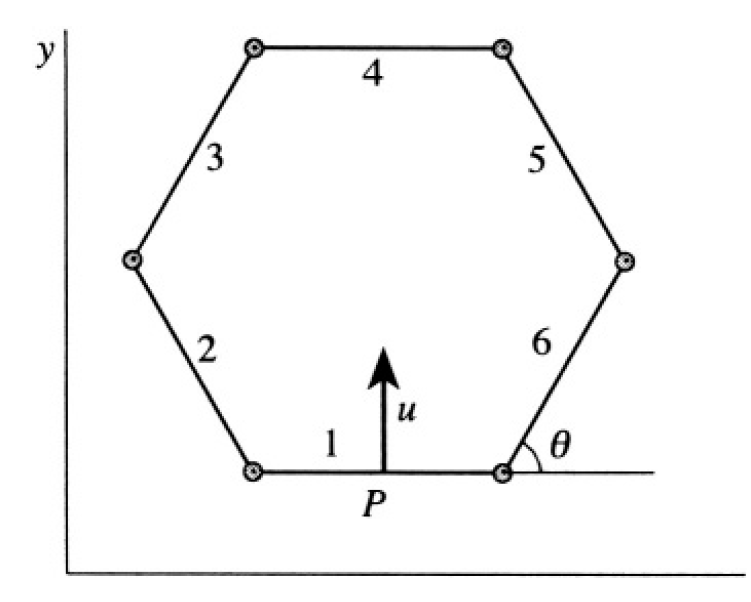
Figure 1.2
rod is u = ẏ The velocity of the midpoint of the opposite one (rod 4) is ẏ + 4aθ cosθ since the coordinates of its center of mass are(x, y + 4a sinθ) We may try to use the condition Pθ = 0 to find a relation between 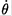 and ẏ. At t = 0, θ = π/3 for a regular hexagon and
and ẏ. At t = 0, θ = π/3 for a regular hexagon and
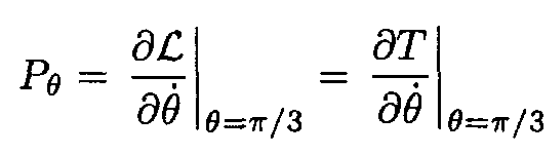
where 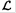 is the Lagrangian of the system, which in this case is equal to its kinetic energy T
is the Lagrangian of the system, which in this case is equal to its kinetic energy T

Where i = 1…6 are subsequent rods (see Figure 1.2). The kinetic energy of each rod consists of its energy relative to the center of mass plus the energy of its center of mass. Let us say that the mass of the rod is m. The energy relative to the center of mass will be the same for rods i = 2, 3, 5, 6 and equal to 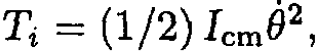 where Icm is the moment of inertia relative to the center of mass. We have already used Icm. To calculate it, we can either integrate (which is very simple in this case) or use a more general approach, which can be applied in other problems with bodies possessing certain symmetries. In this case, we know that the moment of inertia of the rod is γmL2, where L is the length of the rod and γ is some numerical factor. Now move to the edge of the rod. The moment of inertia Ie is
where Icm is the moment of inertia relative to the center of mass. We have already used Icm. To calculate it, we can either integrate (which is very simple in this case) or use a more general approach, which can be applied in other problems with bodies possessing certain symmetries. In this case, we know that the moment of inertia of the rod is γmL2, where L is the length of the rod and γ is some numerical factor. Now move to the edge of the rod. The moment of inertia Ie is
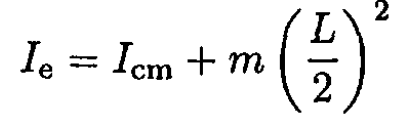
where L /2 is the distance between the edge and the center of mass. Here we have applied the parallel axis theorem. On the other hand, this Ie is nothing but half of the moment of inertia relative to the center of mass of a rod that is twice as long. So, we can write
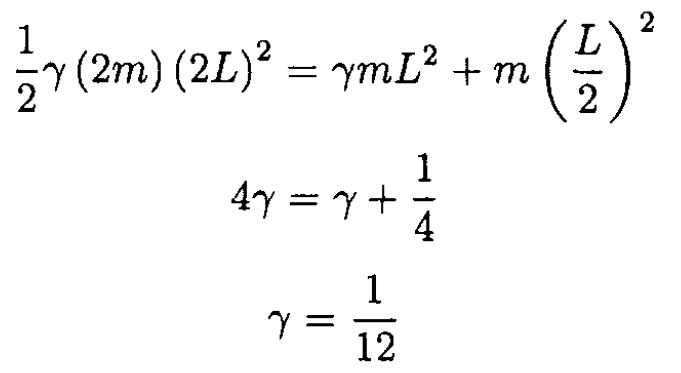
The moment of inertia of the rod is then I = (1/12)mL2. In our case, L = 2a, so I = (1/3)ma2. We then arrive at
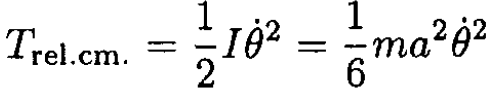
Now calculate the center of mass energy of each rod Ti = (m/2) (ẋ2i + ẏ2i):
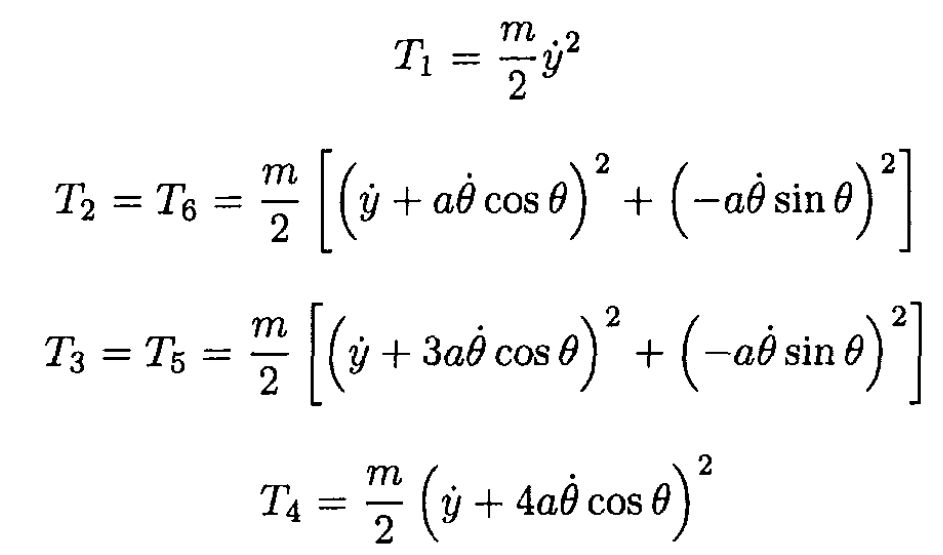
So the total kinetic energy is
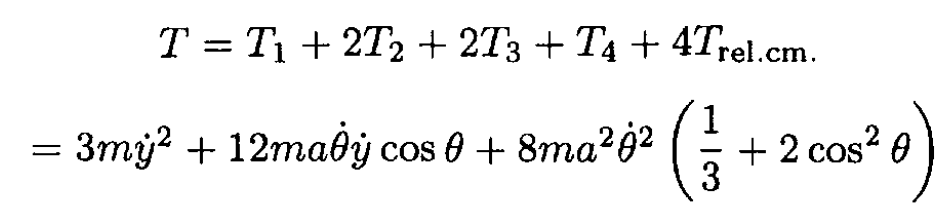
Now we can calculate Pθ at θ = π/3:
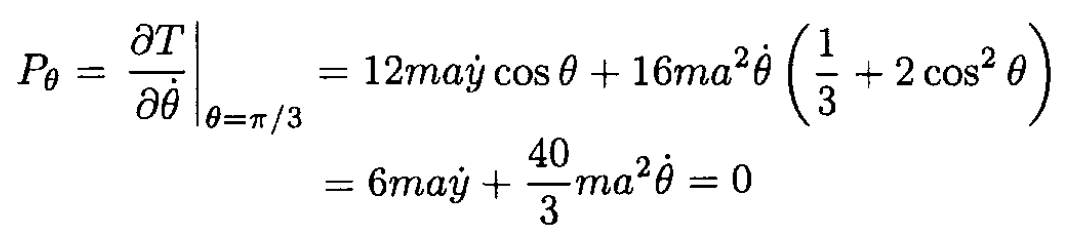
So

Now recalling that ẏ = u, we get for the velocity of rod 4
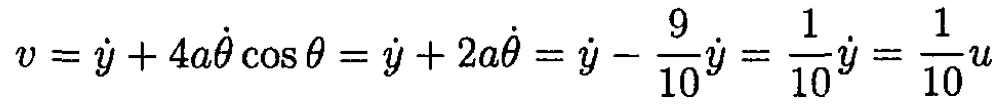



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|