


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 21-8-2016
Date: 1-8-2016
Date: 25-8-2016
|
Concentric Spherical Capacitor
Consider two concentric metal spheres of finite thickness in a vacuum. The inner sphere has radii a1 < a2. The outer sphere has b1 < b2 (see Figure 1.1).
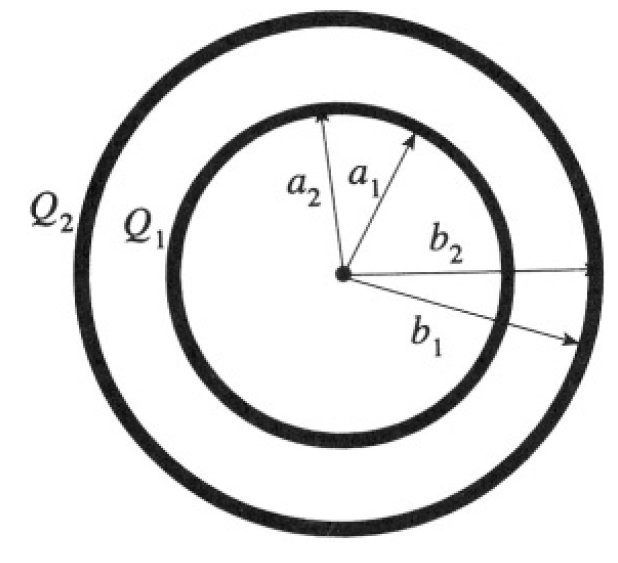
Figure 1.1
a) A charge Q1 is put on the inner sphere and a charge Q2 on the outer sphere. Find the charge density on each of the four surfaces. If Q2 = -Q1 what is the mutual capacitance of the system?
b) If the space between the spheres is filled with insulating material of dielectric constant ε1, what are the surface charge densities and polarization surface charge densities for arbitrary Q1 and Q2 and the mutual capacitance for Q2 = -Q1.
SOLUTION
a) By using Gauss’s theorem and the fact that charges rearrange themselves so as to yield a zero electric field inside the conductors, we infer that all of Q1 will reside on surface 2 of the inner sphere, -Q1 on surface 3 of the outer sphere (no field in the interior of the outer sphere), and Q1 + Q2 on surface 4 of the outer sphere (see Figure 1.2). The surface charge
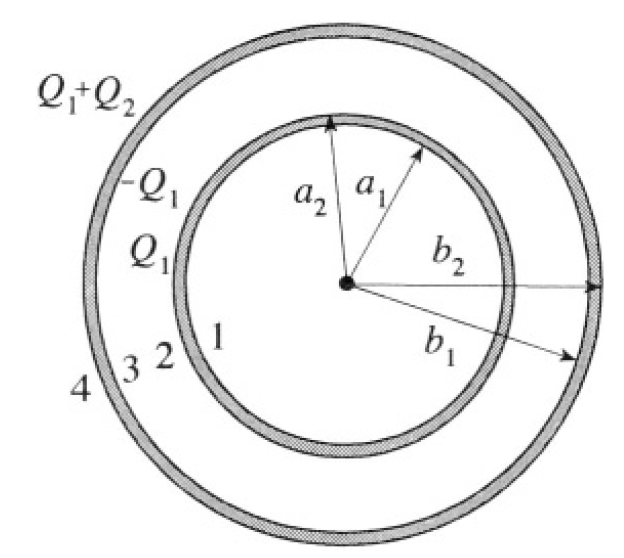
Figure 1.2
densities are straightforward to calculate as the charge divided by surface area:
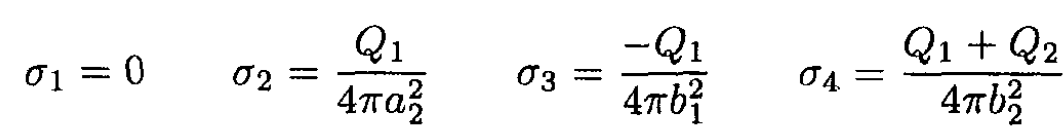
If Q2 = -Q1, there is no charge on the external shell, simply Q1 on surface 2 and –Q1 on surface 3. The mutual capacitance may be calculated from ∆VC = Q1, where ∆V is the difference in electric potential between the spherical shells. Again using Gauss’s theorem to calculate the magnitude E of the electric field between the shells, we have
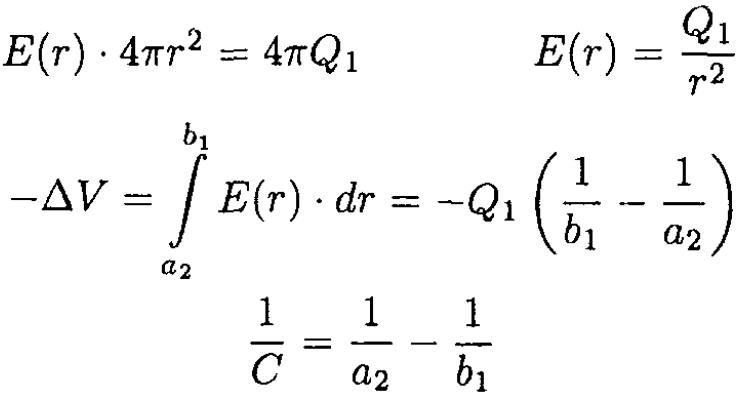
b) The D field behaves like the E field before:
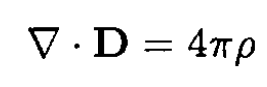
so, between the spheres
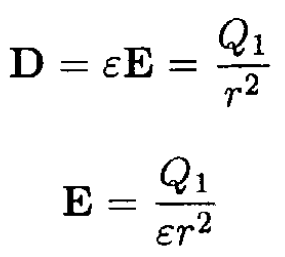
The real and polarization surface charge densities on surface 1 are still zero, and on surface 2, we find
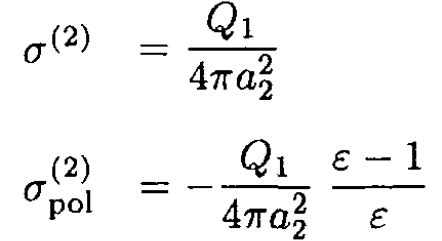
Likewise, on the third and fourth surfaces,
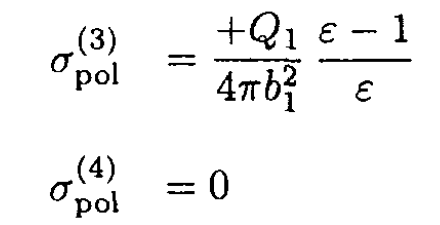
Finally, the capacitance may be found:
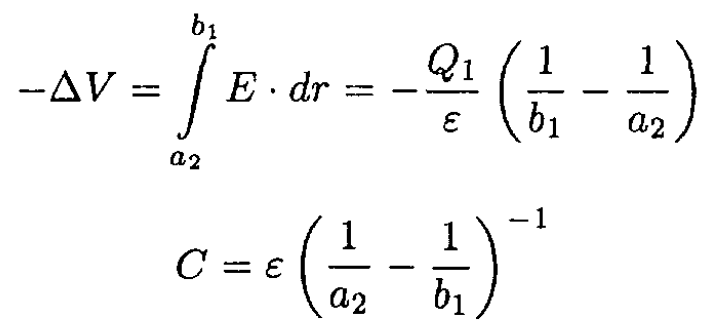



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|