


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-9-2016
Date: 9-8-2016
Date: 2-8-2016
|
Three Masses and Three Springs on Hoop
Three masses, each of mass m are interconnected by identical massless springs of spring constant k and are placed on a smooth circular hoop as
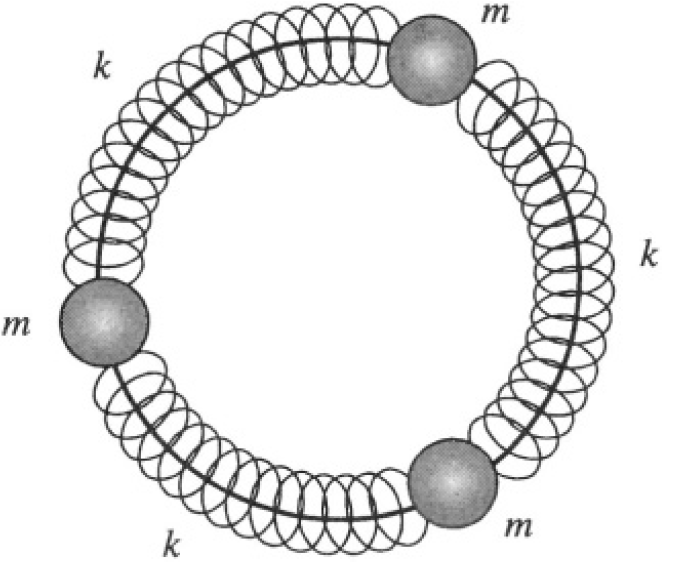
Figure 1.1
shown in Figure 1.1. The hoop is fixed in space. Neglect gravity and friction. Determine the natural frequencies of the system, and the shape of the associated modes of vibration.
SOLUTION
Introducing xi, the displacement from equilibrium for respective masses 1,2,3 (see Figure 1.2), we can write a Lagrangian in the form
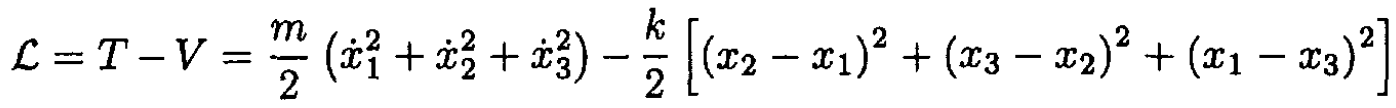
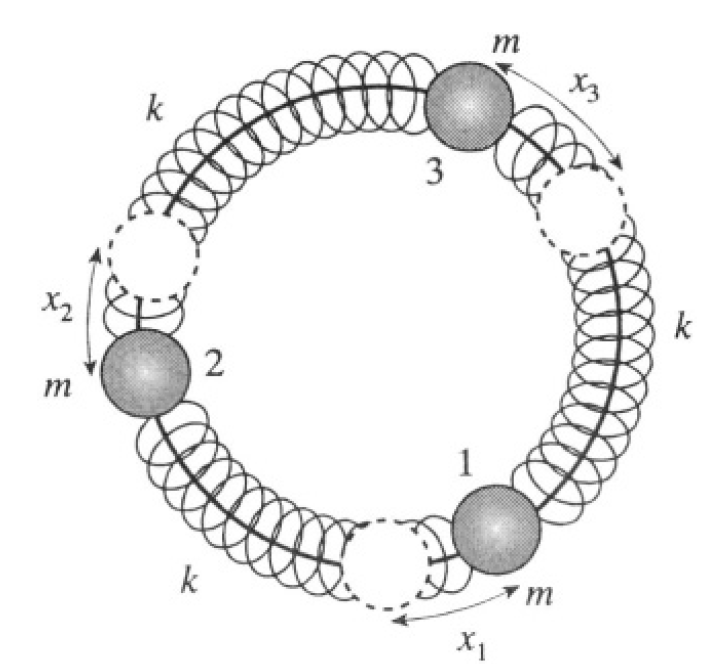
Figure 1.2
The resulting equations of motion are in the form
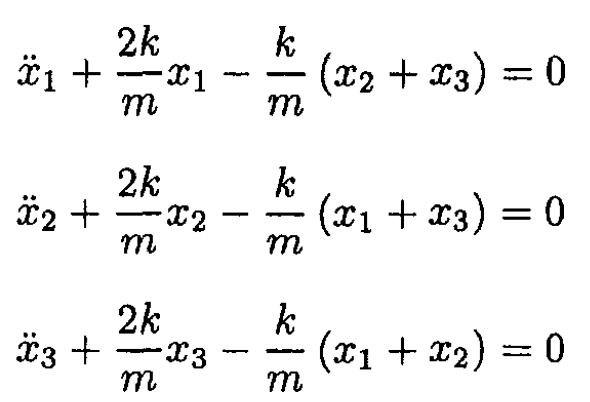 (1)
(1)
Again, looking for solutions of the form xi = Ai eiωt, we obtain an equation for the determinant:
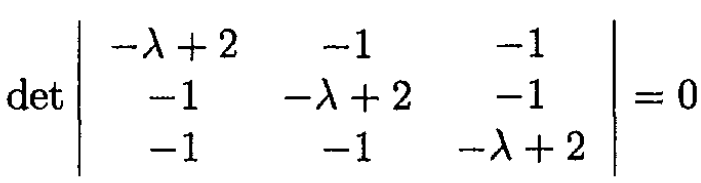
Where λ = ω2/ω20 and ω20 = k/m. The first root is λ1 = ω = 0 which corresponds to the movement of all three masses with the same velocity. The two other roots are 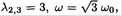 which are double degenerate, corresponding to the mode A1 = 3, A2 = -A3, or A2 = 0, A1 = -A3, where one mass is at rest and the two others move in opposite directions. The result can be obtained even without solving (1), if one can guess that this is the mode. Then
which are double degenerate, corresponding to the mode A1 = 3, A2 = -A3, or A2 = 0, A1 = -A3, where one mass is at rest and the two others move in opposite directions. The result can be obtained even without solving (1), if one can guess that this is the mode. Then
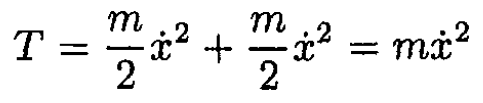
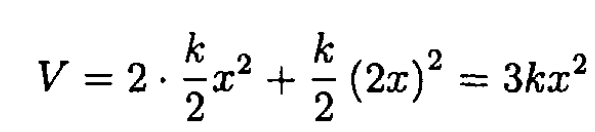
So, again, 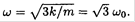



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|