In general, determining the chromatic number of a graph is hard. While small or well-known graphs (like the ones in the previous exercises) may be fairly easy,  the number of possibilities in large graphs makes computing chromatic numbers difficult. We therefore often rely on bounds to give some sort of idea of what the chromatic number of a graph is, and in this section we consider some of these bounds.

If G is a graph on n vertices, then an obvious upper bound on χ(G) is n, since an n-coloring is always possible on a graph with n vertices. This bound is exact for complete graphs, as it takes as many colors as there are vertices to color a complete graph. In fact, complete graphs are the only graphs for which this bound is sharp .We set this aside as Theorem 1.1.

Theorem 1. 1.

For any graph G of order n, χ(G) ≤ n. Let us now discuss a very basic graph coloring algorithm, the greedy algorithm.

To color a graph having n vertices using this algorithm, first label the vertices insome order—call them v₁, v₂, ... , v_n.

Next, order the available colors in some way.Wewilldenotethembythepositiveintegers1,2, ..., n. Then start coloring by assigning color 1 to vertex v1. Next, if v₁ and v₂ are adjacent, assign color2tovertex v2; otherwise, use color 1 again.

In general, to color vertex v_i, use the first available color that has not been used for any of vi’s previously colored neighbors.

For example, the greedy algorithm produces the coloring on the right from the graph on the left in Figure 1. 1. First, v₁ is assigned color 1; then v₂ is assigned color 1, since v₂ is not adjacent to v₁.Then v₃ is assigned color 1 since it is no adjacent to v₁ or v₂.Vertex v₄ is assigned color 2, then v₅ is assigned 2, and finally v is assigned 2.

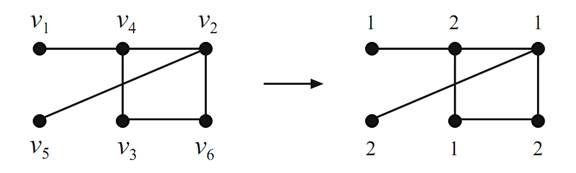
                        FIGURE 1.1. Applying the greedy algorithm.

It is important to realize that the coloring obtained by the greedy algorithm depends heavily on the initial labeling of the vertices. Different labelings can (and often do) produce different colorings. Figure 1.2 displays the coloring obtained from a different original labeling of the same graph. More colors are used in this

                                FIGURE 1.2. Applying it again.

second coloring. We see that while “greed works” in that the algorithm always gives a legal coloring, we cannot expect it to give us a coloring that uses the fewest possible colors.

The following bound improves Theorem 1.1.

Theorem 1.2.

For any graph G, χ(G) ≤ Δ(G)+1,where Δ(G) is the maxi- mum degree of G.

Proof. Running the greedy algorithm on G produces a legal coloring that uses at most Δ(G)+1 colors. This is because every vertex in the graph is adjacent to at most Δ(G) other vertices, and hence the largest color label used is at most Δ(G)+1. Thus, χ(G) ≤ Δ(G)+1.

Notice that we obtain equality in this bound for complete graphs and for cycles with an odd number of vertices. As it turns out, these are the only families of graphs for which the equality in Theorem 1.2 holds. This is stated in Brooks’s Theorem[1]. The proof that we give is a modification of the one given by Lova´asz.

Theorem 1. 3 (Brooks’s Theorem).

If G is a connected graph that is neither an odd cycle nor a complete graph, then χ(G) ≤ Δ(G).

Proof. Let G be a connected graph of order n that is neither a complete graph nor an odd cycle. Let k =Δ(G). We know that k ≠0 and k ≠1, since otherwise G is complete. If k =2,then G must be either an even cycle or a path. In either case, χ(G)=2=Δ(G). So assume that k =Δ(G) ≥ 3.

We are now faced with three cases. In each case we will establish a labeling of the vertices of G in the form v₁, v₂, ... , v_n. We will then use the greedy algorithm to color G with no more than k colors.

Case 1. Suppose that G is not k-regular. Then there exists some vertex with degree less than k. Choose such a vertex and call it v_n. Let S₀ = {v_n} and let S₁ = N(v_n), the neighborhood of v_n. Further, let

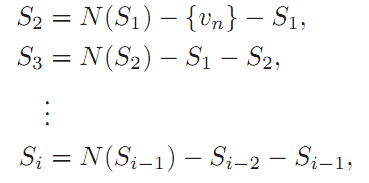
for each i (Figure 1.3). Since G is finite, there is some t such that S_t is not empty,

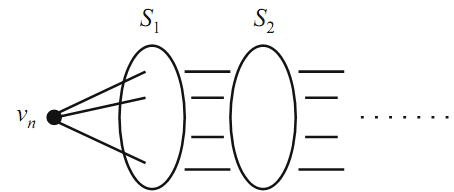
                                                               FIGURE 1.3. The sets S_i.

and S_r is empty for all r>t.

Next, label the vertices in S₁ with the labels v_n−1, v_n−2, ..., v_n−|S1|. Label the vertices in S₂ with the labels v _n−|S1|−1, ..., v _{n−|S1|−|S2|}. Continue labeling in this decreasing fashion until all vertices of G have been labeled. The vertex with label v₁ is in the set S_t.

Let u be a vertex in some S_i, i ≥ 1.Since u has at least one neighbor in S_i−1, it has at most k − 1 adjacencies with vertices whose label is less than its own.

Thus, when the greedy algorithm gets to u, there will be at least one color from {1, 2,...,k} available. Further, since deg(v_n) <k, there will be a color from {1, 2,...,k} available when the greedy algorithm reaches v_n. Thus, in this case the greedy algorithm uses at most k colors to properly color G.

Case 2. Suppose that G is k-regular and that G has a cut vertex, say v. The removal of v from G will form at least two connected components. Say the components are G₁, G₂, ..., G_t. Consider the graph H₁ = G₁ ∪{v} (the component G₁ with v added back—see Figure 1.4).H₁ is a connected graph, and the degree

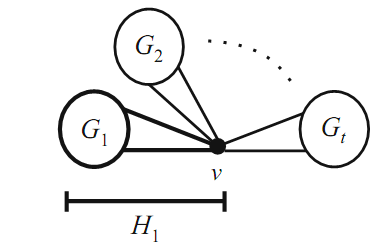
                                                                                   FIGURE 1.4. The graph H₁.

of v in H is less than k. Using the method in Case 1, we can properly color H1 with at most k colors. Similarly, we can properly color each H_i = G_i −{v} with at most k colors. Without loss of generality, we can assume that v gets the same color in all of these colorings (if not, just permute the colors to make it so). These colorings together create a proper coloring of G that uses at most k colors. Case 2 is complete.

Case 3. Suppose that G is k-regular and that it does not contain a cut vertex. This means that G is 2-connected.

Subcase 3a. Suppose that G is 3-connected. This means that for all v, the graph G − v is 2-connected. Let v beavertex of G with neighbors v₁ and v₂ such that v₁v₂ ∉ E(G) (such vertices exist since G is not complete). By the assumption in this subcase, the graph G −{v₁,v₂} is connected.

Subcase 3b. Suppose that G is not 3-connected. This means that there exists a pair of vertices v,w such that the graph G −{v,w} is disconnected. Let the components of G −{v, w} be G₁, G₂, ..., G_t. Since k ≥ 3, it must be that each G_i has at least two vertices. It also must be that v is adjacent to at least one vertex in each G_i, since w is not a cut vertex of G. Let u ∈ V (G₁) be a neighbor of v. Suppose for the moment that u is a cut vertex of the graph G − v. If this is the case, then there must be another vertex y of G₁ such that (i) y is not a cut vertex of the graph G−v, and (ii) the only paths from y to w in G−v go through vertex u. Since u is not a cut vertex of G itself, it must be that y is adjacent to v. In either case, it must be that v has a neighbor in G₁ (either u or y) that is not a cut vertex of G −v. The vertex v has a similar such neighbor in G₂. For convenience, let us rename: For i =1, 2,let v_i ∈ V (G_i) be a neighbor of v that is not a cut vertex of the graph G − v. Vertices v₁ and v₂ are nonadjacent, and since they were in different components of G −{v,w}, it must be that G −{v₁,v₂} is connected.

In each subcase, we have identified vertices v, v₁,and v₂ such that vv₁,vv₂ ∈ E(G), v₁v₂ ∉E(G),and G −{v₁,v₂} is connected. We now proceed to label the vertices of G in preparation for the greedy algorithm.

Let v₁ and v₂ be as labeled. Let v be labeled v_n. Now choose a vertex adjacent to v_n that is not v₁ or v₂ (such a vertex exists, since deg(v_n) ≥ 3). Label this vertex v_n−1. Next choose a vertex that is adjacent to either v_n or v_n−1 and is not v₁, v₂, v_n,or v_n−1. Call this vertex v_n−2. We continue this process. Since G −{v₁,v₂} is connected, then for each i ∈{3,...,n − 1},there is a vertex v_i ∈ V (G) −{v₁,v₂,v_n,v_n−1,...,v_i+1} that is adjacent to at least one of v_i+1,...,v_n.

Now that the vertices are labeled, we can apply the greedy algorithm. Since v₁v₂ ∉ E(G), the algorithm will give the color 1 to both v₁ and v₂. Since each v_i, 3 ≤ i<n, is adjacent to at most k − 1 predecessors, and since v_n is adjacent to v₁ and v₂, the algorithm never requires more than k =Δ(G) colors. Case 3 is complete.

 The next bound involves a new concept.

The clique number of a graph, denoted by ω(G), is defined as the order of the largest complete graph that is a subgraph of G. For example, in Figure 1.4,  ω(G₁)=3 and ω(G₂)=4.

FIGURE 1.4. Graphs with clique numbers 3 and 4, respectively.

A simple bound that involves clique number follows. We leave it to the reader to provide a (one or two line) explanation.

Theorem 1.4. For any graph G, χ(G) ≥ ω(G).

It is natural to wonder whether we might be able to strengthen this theorem and prove that χ(G)= ω(G) for every graph G. Unfortunately, this is false. Consider the graph G shown in Figure 1.5. The clique number of this graph is 5, and the

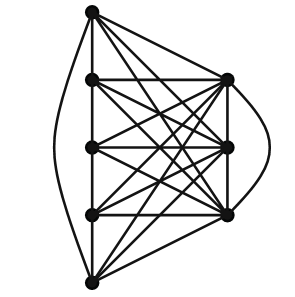
                                                                            FIGURE 1.5. Is χ(G)= ω(G)?

chromatic number is 6 (see Exercise 2).

The upper and lower bounds given in Theorem 1.5 concern α(G), the independence number of G,. The proofs are left as an exercise (see Exercise 3).

Theorem 1.5. For any graph G of order n,

_________________________________________________________________________________

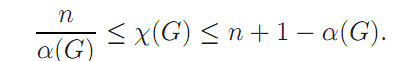
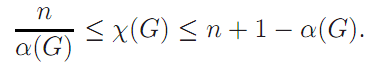
1-Graph Theory  and Applications ,Jean-Claude Fournier, WILEY, page(76)

2-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(88-93)