


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-02-06
التاريخ: 28-12-2016
التاريخ: 10-8-2017
التاريخ: 23-2-2016
|
تردد الحركة التوافقية البسيطة
يعتبر إيجاد تعبير لتردد الحركة التوافقية البسيطة باستعمال حساب التفاضل والتكامل مسألة مباشر تماما.
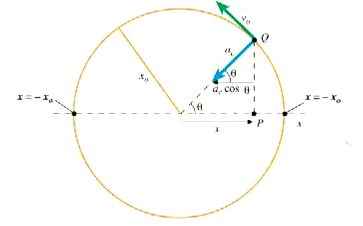
الشكل ((1: عندما يتحرك الجسيم Q على محيط دائرة نصف قطرها x0 بسرعة ثابتة المقدار v0، تتحرك النقطة P حركة توافقية بسيطة من –x0 ≤ x ≤ x0 ، ونظراً لأن نصف قطر الدائرة x0 ، اذن x = x0 cos θ.
سوف نبدأ بتخيل جسيم Q يتحرك بسرعة v0 المقدار في دائرة نصف قطرها x0. هذه الدائرة تسمى دائرة الاسناد، ويمثل الشكل (1) رسما تخطيطيا لهذه الحركة. ويمكن أيضا وصف حركةQ بأنها حركة ذات سرعة زاوية /Δt = ωθΔ ثابتة تعطى بالعلاقة = v0/x0ω , أن ω تقاس بالزاوية نصف القطرية لكل ثانية . وكلن الدورة T التي يصنع خلالها الجسيم Q دورة كاملة هي الزمن اللازم للدوران حول الدائرة مرة واحدة ، أو:
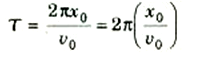
إذن ، تردد الحركة f ، أي عدد الدورات لكل ثانية , هو مجرد مقلوب الدورة:
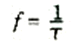
لا حظ في الشكل 1)) أن النقطة p تمثل موضع مسقط الجسيمQ على المحور x ، حيث x = x0 cos θ لأي قيمة للإحداثي x ومعنى ذلك أنه عندما يدور الجسيم q على محيط الدائرة دورة كاملة فإن p تتحرك على استقامة المحور x من يوجد معادلة الى –x ثم تعود الى +x0 بنفس الدورة وبنفس التردد كالجسيم Q تماما وسوف نثبت الان أن p تتحرك SHM .
تعطى العجلة الطاردة المركزية للحركة الدائرة للجسيم Q بالعلاقة:
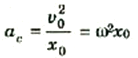
لاحظ أن هذه العجلة ac تعمل في اتجاه نصف القطر الى داخل , كما هو مبين بالشكل ( (1وبناء على ذلك فإن العجلة المناظرة للنقطة P تساوي مركبة ac في اتجاه المحور X:
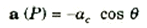
وتعني الإشارة السالبة أن عجلة النقطة p , أي (p)a تؤثر في الاتجاه السالب للمحور x . إذن ، باستخدام التعبير الخاص بالعجلة الطاردة المركزية ac والعلاقة معادلة نحصل على:
1)) 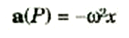
حيث w ثابتة . هذا يثبت أن النقطة P تتحرك SHM , وذلك لان العلاقة a = -kx تمثل الصورة العاملة لعجلة الحركة التوافقية البسيطة.
الآن أصبح إيجاد تردد الحركة التوافقية البسيطة عموما مسألة في غاية البساطة ، فبأستعمال المعادلة (1) نجد أن:

حيث k ثابت القوة. وهكذا يمكن تعريف ω كالتالي :
2)) 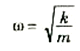
إذن , تردد الحركة التوافقية البسيطة للنقطة P هو:
(3) 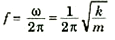
كما أن دورة الحركة التوافقية البسيطة هو:
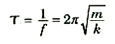 (4)
(4)
وحيث أن هذا الاشتقاق لا يختص بمثال محدد للحركة التوافقية البسيطة ، يمكننا إذن استنتاج ان المعادلتين (3) و(4) هما التعبيران العامان لتردد ودورة أي نظام يتحرك SHM وعليه ، إذا أمكننا إيجاد ثابت القوة h لنظام معين , يمكننا إيجاد f وτ لهذا النظام مباشرة.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل: شراكتنا مع المؤسّسات الرائدة تفتح آفاقًا جديدة للارتقاء بجودة التعليم الطبّي في العراق
|
|
|