


 النبات
النبات
 الحيوان
الحيوان
 الأحياء المجهرية
الأحياء المجهرية
 علم الأمراض
علم الأمراض
 التقانة الإحيائية
التقانة الإحيائية
 التقنية الحيوية المكروبية
التقنية الحيوية المكروبية
 التقنية الحياتية النانوية
التقنية الحياتية النانوية
 علم الأجنة
علم الأجنة
 الأحياء الجزيئي
الأحياء الجزيئي
 علم وظائف الأعضاء
علم وظائف الأعضاء
 الغدد
الغدد
 المضادات الحيوية
المضادات الحيوية|
Read More
Date: 20-4-2016
Date: 17-4-2016
Date: 19-4-2016
|
Buffers
Proteins have a pH dependent charge and many of the properties of proteins change with pH. Consequently, in working with proteins, it is important to control the pH. This is achieved by the use of buffers, and so at the outset it is important to have some insight into buffers, to know which buffer to use for any particular purpose, and how to make up the buffer.
Buffers are solutions of weak acids or bases and their salt(s), which resist changes in pH. Weak acids and bases are distinguished from strong acids and bases by their incomplete dissociation. In the case of a weak acid the dissociation is:-
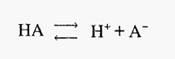
and the dissociation constant is:-
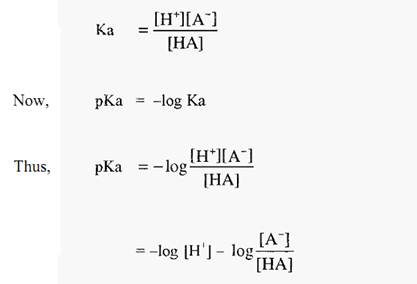
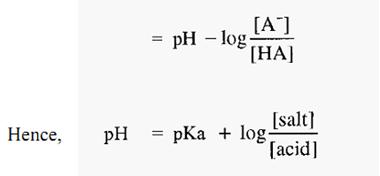

For a weak base (e.g. Tris) the dissociation is:-
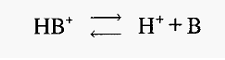
Using similar arguments to those above, it can be shown that in this case,
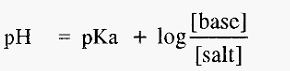

Equations 1 and 2 are forms of the Henderson-Hasselbalch equation, which can be written in a general form as:-
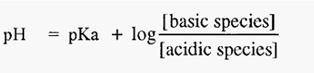

From which it can be seen that, when [basic species] = [acidic species], then,
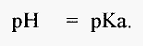
A simple monoprotic weak acid, such as acetic acid, yields a titration curve such as that shown schematically in Fig. 1. It will be noticed that when pH = pKa, the solution resists changes in pH, i.e. it functions best as a buffer in the range pH = pKa ± 0.5.
CH3COOH is the acidic species in this buffer and CH3COO- is the basic species. It may be observed that a solution of acetic acid itself (CH3COOH) will have a pH less than the pKa of acetic acid. Conversely, a solution containing only sodium acetate will have a pH greater than the pKa of acetic acid. It is important to understand this point in order to appreciate how to make an acetate buffer using the approach described in Section 1.1.
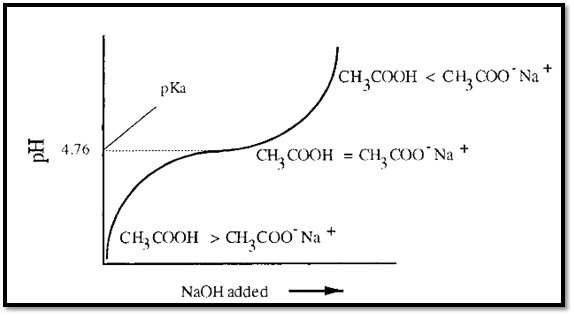
Figure 1. Schematic titration curve of a monoprotic acid, such as acetic acid.
A triprotic acid, such as phosphoric acid will yield a titration curve having three inflexion points (Fig. 2), corresponding to the three pKa values of phosphoric acid.
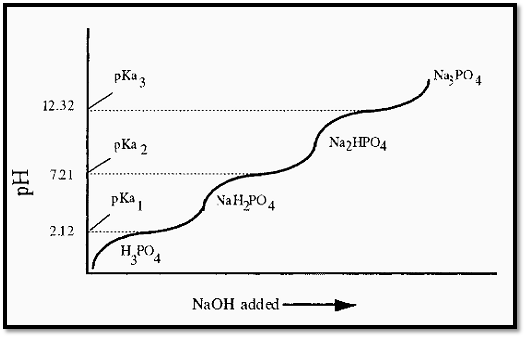
Figure 2. Schematic titration curve of phosporic acid.
For most biochemical purposes, pKa2 is of greatest interest, since it is Note that:-closest to the pH of the extracellular fluid of animals.
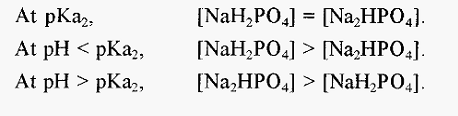
Put another way, a solution NaH2PO4 will have a pH less than pKa2and a solution of Na2HPO4 will have a pH greater than pKa2. It is important to understand this point in order to appreciate how to make a phosphate buffer using the approach described below.
1.1 Making a buffer
A simple approach to the making of a buffer is described below. The advantage of this approach is that only one solution needs be made up. Several books suggest that buffers should be made up by adding “x” ml of a 1 M solution of “A” to “y” ml of a 1 M solution of “B”. The problem with this approach is that it involves extra work (making up two solutions when one will do), waste (the unused volumes of “A” and “B” are discarded) and is usually inaccurate (the presence of extra salts and preservatives, for example, can change the pH due to common ion effects).
A simpler method follows the following steps:-
• Choose the buffer. A buffer works best at its pK, so the first step is to choose a buffer with a pKa as close as possible to the desired pH.
• Identify the buffering species. a buffer consists of two components: a weak acid and its salt or a weak base and its salt. The second step is thus to identify the species which will constitute the buffer. For example, in the case of an acetate buffer, the buffering species are CH3COOH and CH3COONa. In a phosphate
buffer at pKa2, the buffer species are NaH2PO4 and Na2HPO4.
• Identify whether the buffer is made from an acid or a base. The two buffer examples shown above are made from acids, acetic acid or phosphoric acid. In the case of phosphate buffer at pKa2, the acid is NaH2PO4. An example of a buffer made from a base is Tris/Tris-HCl, which buffers best at pH 8.1, the pKa of Tris.
• Choose the species that gives no by-products when titrated. Almost all buffers can be made up by weighing out one component, dissolving in a volume just short of the final volume, titrating to the right pH, and making up to volume. It is not necessary to make up separate solutions of the two buffer constituents - the required salt can be generated in situ by titrating the acid with an appropriate base - or vice versa in the case of a buffer made from a base. [Remember: Titrate an acid “up” (i.e. with a strong base) and titrate a base “down” (i.e. with a strong acid)].
Remember, acid + base = salt + water
and, a buffer = (acid + its salt ) or (base + its salt).
The term “its salt” is important. For example, if we wanted to make an acetate buffer, it is easy to identify that this buffer is made from acetic acid and its salt, say, sodium acetate. But,
Q: Could the required mixture of CH3COOH and CH3COONa be made
by titrating a solution of CH3COONa to the correct pH with HCl?
A: No! Because the reaction in this case is:-
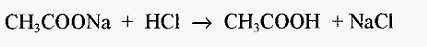
and the resultant solution contains NaCl, which is an unwanted by-product and which is not a salt of acetic acid (i.e. it is not “its salt”). On the other hand,
Q: Could the required mixture be made by titrating a solution of
A: Yes! The reaction in this case is:-CH3COOH with NaOH?
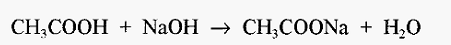
which yields only the salt of acetic acid and water, i.e. there are no by-products. Similarly, in the case of a phosphate buffer, if one chooses Na2HPO4, the pH of a solution of this salt will be higher than pKa, (see Fig. 2) and this will require titration with an acid. If one chooses HCl, the reaction will be:-
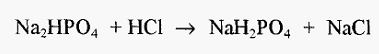
which yields NaCl as an unwanted by-product. (And if one chooses NaH2PO4, this will change the phosphate molarity.) However, if one starts with NaH2PO4, the pH of a solution of this salt will be lower than pKa, and this will require titration with a base. If one chooses NaOH, the reaction will be:-
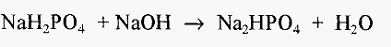
volume. For example, the molarity of a phosphate buffer is determined by the molarity of the phosphate moiety, which does not change when NaH2PO4 is titrated to Na2HPO4. If a litre of a 0.1 M buffer is required, then 0.1 moles of NaH2PO4 can be weighed out.
• Add all other components, titrate and make up to volume. Buffers
often contain ingredients other than the two buffering species. For ion-exchange elution the buffer might contain extra NaCl, and buffers often contain preservatives such as NaN3 or chelating agents such as EDTA. Except for NaN3, these should all be added before the titration. All constituents should be dissolved in the same solution to just less than the final volume, i.e. a volume must be left for the titration but the final dilution after titration should be as small as possible. (The Henderson-Hasselbalch equation predicts that the pH of a buffer should not change with dilution, but this is only true over a small range, due to non-ideal behaviour of ions in solution.) Finally the solution is titrated to the desired pH and made up to volume.
NaN3 should be added after titration as it liberates the toxic gas, HN3, when exposed to acid. Manganese salts should also be added after adjustment of the pH as these may form irreversibly insoluble salts at pH extremes.
1.2 Buffers of constant ionic strength
Besides pH, which influences the sign and magnitude of the charge on a protein, proteins are also influenced by the specific ions present in solution and by the solution ionic strength. In a buffer, the pH and the ionic strength are related. The Henderson-Hasselbalch equation, for a buffer made from an acid, is:-
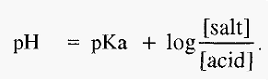
The ionic strength of the buffer is a function of the [salt]. Therefore, in this case as the pH rises, the buffer ionic strength also rises. Ionic strength is also a function of the molarity of the buffer. One can picture the relationship between the three variables, molarity (M), pH and ionic strength (I) as a lever, for which any one of the three could be fixed as a fulcrum and the relative movements of the other two observed (Fig. 3).
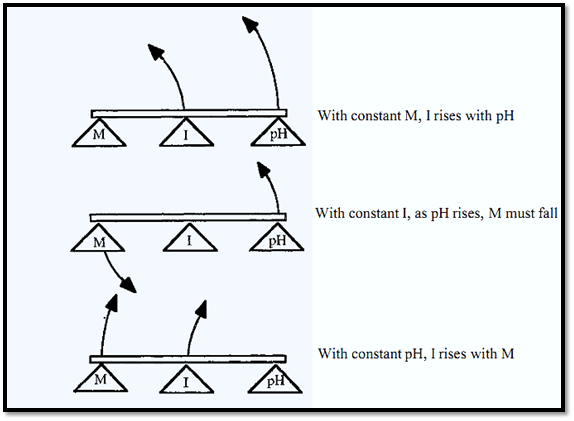
Figure 3. The relationship between molarity, pH and ionic strength for a buffer made from a weak acid.
For a buffer made from a weak base, the relevant form of the Henderson-Hasselbalch equation is:-
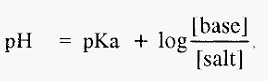
In this case, therefore, the ionic strength increases as the pH decreases and the relationship between “M” (molarity), “I” (ionic strength) and pH can be visualized by reversing the positions of M and I in Fig. 3. The lever model shown in Fig. 5 must not be taken to imply a linear relationship between the variables. In fact, ionic strength changes sigmoidally with pH as shown in Fig. 4. The “rate” of change, i.e. d(ionic strength) ld (pH), is greatest at the pKa, pKa2 in this case. The pKa itself also changes slightly with ionic strength. The data in Fig.4 were calculated according to Ellis and Morrison.
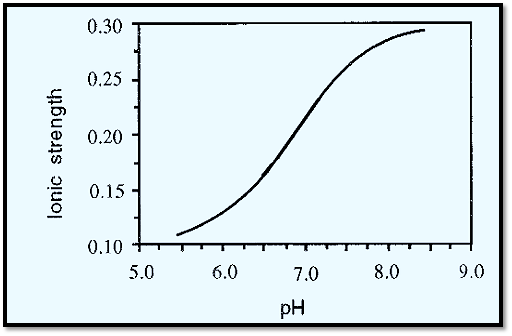
Figure 4. The relationship between ionic strength and pH for a 0.1 M phosphate buffer.
The relationship between pH, M and I is important when establishing the pH optimum of an enzyme. This is commonly done by using a range of buffers of constant M and varying pH. However, if the enzyme in question is affected by ionic strength (which is often the case) it is better to keep I constant and to vary M with pH (For an example, see ref. 4). The preparation of buffers of constant ionic strength is discussed by Ellis and Morrison2. An in depth discussion of buffers is provided by Perrin and Dempsey5.
References
Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .
Ellis, K. J. and Morrison J. F. (1982) Buffers of constant ionic strength for studying pH-dependent processes. Methods Enzymol. 87, 405-426.
Scopes, R. K. (1994) Protein Purification: Principles and Practice. 3rd Ed, Springer-Verlag, New York, pp326-330.
Dehrmann, F. M., Coetzer, T. H. T., Pike, R. N. and Dennison, C. (1995) Mature cathepsin L is substantially active in the ionic milieu of the extracellular matrix. Arch. Biochem. Biophys. 324, 93-98.
Perrin, D. D. and Dempsey, B. (1974) Buffers for pH and metal ion control. Chapman and Hall, London.

|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|