نتائج إضافية على الأنظمة الخطية وقابلية للانعكاس:

نقدم في هذا البند إضافية للأنظمة الخطية وقابلية انعكاس المصفوفات. علاوة على معرفة طريقة جديدة لحل n من المعادلات التي تحتوي على n من المتغيرات.

مبرهنة (1-1):

نظام المعادلات الخطية:

1. ما لا يحتوي على حل.

2. او يحتوي على حل واحد فقط.

3. أو له عدد غير منتهي من الحلول.

البرهان:

ليكن Ax = B نظام لمعادلات خطية، فإن بالضبط واحد من الاحتمالات أعلاه يكون صحيحاً. نفرض أن النظام Ax = B له اكثر من حل و x_○ =x₁-x₂ حيث x₂ , x₁ حلان معينان للنظام. عليه فإن x_o لا يساوي صفر، إضافة لذلك:

وإذا افترضنا K ثابت فإن:

  بما ان x_n لا يساوي صفر فإن Ax = R له اكثر من حل.

لقد قدمنا في البنود السابقة طريقتين، لحل النظام الخطي هما:

1. طريقة حذف كاوس.

2. طريقة حذف كاوس ــ جوروان.

وسنقوم بتوضيح طريقة أخرى لحل النظام الخطي.

مبرهنة (1-2):

إذا كانت A مصفوفة سعتها  n x n وقابلة للانعكاس ، فإن النظام الخطي AX = B له حل واحد فقط.

                                                                   X = A^-1B

البرهان:

بما أن A(A^-1B) = B ، فإن A^-1B هو حل للمعادلة AX = B. ولكي نثبت بأنه الحل الوحيد، نفرض أن X₁ هو حل آخر لا على اليقين.

لذا فإن AX₁ = B، بالضرب في A^-1 نحصل على X₁ = A^-1B . ومنها X₁ = X.

مثال(1):

حل النظام الآتي:

الحل:

1. نكتب النظام أعلاه بالشكل AX = B.

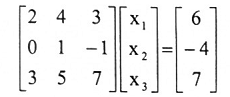
2. توجد معكوس المصفوفة A بإحدى الطرق السابقة.

3. الحل هو:

أو:

                                      X₃ = -4      ,   X₂ = -8       ,   X₁ = 25

مبرهنة (1-3):

لتكن A مصفوفة مربعة

1. إذا كانت المصفوفة المربعة B تحقق BA = I_n فإن B = A^-1

2. إذا كانت المصفوفة المربعة B تحقق  AB = I_n فإن B = A^-1

البرهان:

نفرض BA = I_n، بضرب الطرفين من جهة اليمين في A^-1 نحصل على BAA = IA أو BI = IA

مبرهنة (1-4):

إذا كانت A مصفوفة مربعة سعتها n x n ، فإن الصيغ الآتية متكافئة.

A  .1 قابلة للانعكاس.

AX = 0   .2 لها حل واحد هو الحل الصفري.

3. الصيغة المدرجة المختزلة للمصفوفة A هي I_n.

4. يمكن كتابة A كحاصل ضرب مصفوفات بسيطة.

5.  النظام AX = B  متسق لكل مصفوفة B ذات السعة n x 1 .

مثال (2):

ما هي الشرط على b₃,b₂,b₁ لكي يكون النظام الآتي منسقاً.

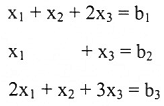
الحل:

باستخدام عمليات صف بسيطة على  المصفوفة الممتدة.

واضح من شكل المصفوفة أعلاه أن النظام الخطي متسق إذا تحقق الشروط:

بمعنى آخر أن النظام الخطي AX = B متسق إذا وفق إذا كانت: