


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2021
Date: 1-9-2021
Date: 16-9-2021
|
We now discuss (binary) codes in general.
Any binary string (that is, string of 0s and 1s) can be used to encode information, so we will call any such string a binary codeword. The number of symbols in the string is called its length. The distance between two binary codewords is defined to be the number of places in which they differ. For example, 1010111 and 1100101 are binary codewords of length 7, and the distance between them is 3, because they differ in the second, third and sixth places.
By a binary code we mean a set of binary codewords. Usually we shall just say “code”; while codes based on a set with more than two symbols are used, binary codes are by far the most common. In most cases, we shall require all words in a code to be of same length (but there are a few important exceptions).
The minimum distance between any two codewords in a code (that is, the smallest of all differences between two codewords) is called the minimum distance of the code.
As an example, here is a code with four words:
A =1010101
B =0101010
C =1110000
D =0001111
The distances between the words are
A to B : 7 B to C : 4
A to C : 3 B to D : 3
A to D : 4 C to D : 7
So the minimum distance is 3.
The weight of a codeword is the number of 1s it contains. That is, it is the distance from 000...00. The weight of a code is the minimum weight of all its non-zero words. If 000... is in the code, you do not include it in calculating the minimum weight.
In the preceding example:
A = 1 0 1 0 1 0 1 ; weight is : 4
B = 0 1 0 1 0 1 0 ; weight is : 3
C = 1 1 1 0 0 0 0 ; weight is : 3
D = 0 0 0 1 1 1 1 ; weight is : 4.
This code has weight 3.
The binary sum or join or bit sum or simply sum of two binary sequences is defined as follows.
To add symbols, use the “cancellation” rule
0+0 = 0 0+1 = 1
1+0 = 1 1+1 = 0
In other words, the sum is 1 if the symbols are different and 0 if they are the same. To add sequences (for example, codewords) add terms separately, but there is no carry:

So the distance between two sequences is the weight of their sum. The sum of any binary string with itself is the string 000. . . , and as one would expect the distance between a string and itself is zero.
Some writers use different symbols such as ⊕ or⨀to represent binary sums, but no confusion should arise if we simply use the ordinary plus sign. The binary sum obeys the ordinary associative and commutative laws. We shall denote the string of all zeros as O; if A is any binary string, A+O = A and A+A = O.
Suppose A and B are any two binary sequences of the same length and C is their sum: A + B = C. Then A + B +C = C +C = O. Moreover, A +C = A + O +C = A+B+B+C = O+B = B and B+C = A.
A very important example is the Hamming code of length 7. It is derived from the 16 possible strings of length 4 (of 0s and 1s). To form a 16-word binary code with words of length 7, do Venn diagram encoding on each string.
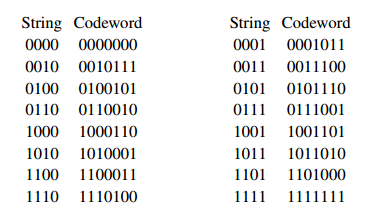
This code—which is called the Hamming code of length 7—is an example of a linear code. The 16 codewords are precisely the strings that we would assume were the intended codewords when we decode a string using Venn diagram decoding.
A linear code is one in which the binary sum of any two of the codewords is also a codeword. Clearly all the words in a liner code must be of the same length (or else the sum will not always be defined).
Many linear codes are derived by:
• taking all strings of some fixed length;
• adding check digits;
• possibly changing the order of the digits in some consistent way.
However, not all linear codes are derived in this way.
Here are two important properties of linear codes. First, the all-zero word 000. . . is always one of the codewords. Second, the minimum distance of the code is equal to the weight of code.
Nearest-neighbor decoding is the following process: find the codeword whose distance from the received message is smallest; decode to that codeword.
Venn diagram decoding is an example of nearest-neighbor decoding. When we explained how to derive the intended message from any seven-digit binary string, we could always derive a codeword by leaving the string unchanged or making one change.
If there were two errors, Venn diagram decoding would give the wrong answer.
But it would at least see that there had been an error. If three errors were made, you might not see the error (because it is possible to get another codeword by this process). That is, Venn diagram decoding (detects and) corrects 1 error in a word, and detects any 2 errors. We say it is a single error correcting, double error detecting code. In a single error correcting code, if the string is not a codeword, then the position whose symbol must be changed in order to make it a codeword is unique.
If a code has minimum distance t, it will detect any (t −1) errors (or fewer) and correct any (t −1)/2 errors (or fewer). Alternatively, we could say that a code with minimum distance t will detect up to (t −1) errors and correct up to (t −1)/2 errors.
Sample Problem 10.2 Consider the code with four words:
A = 1010101
B = 0101010
C = 1110000
D = 0001111
How many errors can this code correct? How many can it detect?
Solution. The code has minimum distance 3. So it detects any 2 errors, corrects any 1 error.
There is no such thing as half an error. So, if your arithmetic tells you that a code can detect up to 2 1/2 errors, the maximum number it will actually detect is 2.
Sample Problem 1.1 Consider the code with words:
A = 11110000
B = 11001100
C = 00110011
D = 00000000
What is the most errors can this code correct? What is the most it can detect?
Solution. The code has minimum distance 4. So it detects any 3 or fewer errors.
It corrects “up to 1.5 errors”, but as you can only have whole numbers of errors, it can only detect 1 error.
The Hamming code has one particular property that is not true of many codes.
Given any string of seven binary digits, there is exactly one codeword that is distance 0 or 1 from the string: either the string is a codeword, or there is a unique codeword into which it can be converted by changing one symbol. We shall call this the unique correction property.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مستشفى العتبة العباسية الميداني في سوريا يقدّم خدماته لنحو 1500 نازح لبناني يوميًا
|
|
|