المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | مستوى ديكارتي Cartisian Plane |
 16148
 02:54 صباحاً
التاريخ: 13-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 311|
أقرأ أيضاً
التاريخ: 14-11-2015
1410
التاريخ: 3-11-2015
1367
التاريخ: 11-1-2016
1756
التاريخ: 3-11-2015
1192
|
يسمى السطح البياني وينسب إلى العالم الفرنسي ديكارت ( 1596 – 1650 ) م مبتكر الهندسة التحليلية , وهو المستوى الناتج عن تقاطع مستقيمين متعامدين الأول أفقي يسمى محور السينات وهو يمثل خط الأعداد الحقيقية والثاني رأسي يمسى محور الصادات ويمثل خط الأعداد الحقيقية أيضاً كما في الشكل .
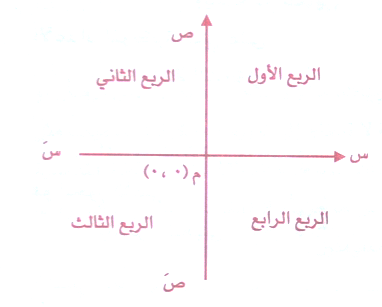
إذا يتقاطعان في نقطة واحدة هي نقطة الأصل م ( 0 ، 0 ) .
فإذا اتجهنا من م إلى اليمين فالإحداثيات موجبة .
وإذا اتجهنا من م إلى اليسار = سالبة .
وإذا اتجهنا من م إلى الأعلى = موجبة .
وإذا اتجهنا من م إلى الأسفل = سالبة .
وكل نقطة في المستوى تمثل زوجاً مرتباً واحداً ينتمي إلى مجموعة حاصل الضرب الديكارتي للأعداد الحقيقية ح × ح ، إذ هناك اقتران تناظر بين الازواج المرتبة عناصر مجموعة الضرب الديكارتي ح × ح ونقاط المستوى الديكارتي .
ولكل زوج مرتب مثل (س ، ص) يسمى الاحداثي السيني بالمسقط الأول .
ويسمى الاحداثي الصادي بالمسقط الثاني .
والمحوران الإحداثيان ( الخطان المتعامدان) يقسمان السطح البياني إلى أربعة أرباع كما في الشكل وهي الربع الأول والثاني والثالث والرابع .
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
