المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | قطوع مخروطية Conic Sections |
 3250
 01:51 صباحاً
التاريخ: 25-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 239|
أقرأ أيضاً
التاريخ: 20-11-2015
917
التاريخ: 17-12-2015
1010
التاريخ: 3-12-2015
1244
التاريخ: 26-11-2015
898
|
القطوع المخروطية من أهم مواضيع الهندسة التحليلية على الإطلاق كونها أهم وسيلة عملية لدراسة الفضاء الخارجي وعى وجه الخصوص مسارات الكواكب والمذنبات والأرض والقمر على السواء , عملياً يمكن الحصول عليها من قطع مستوى لمخروط مزدوج مكون من مخروطين بالرأس ملتقيين .
كما في الشكل .
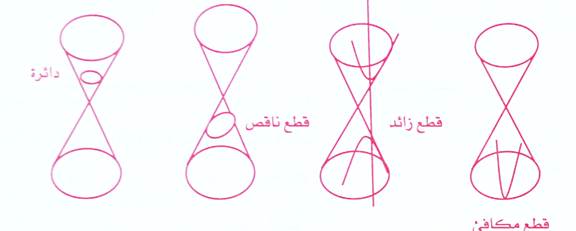
ورياضياً فإن منحنياتها تمثل نوعاً من العلاقات الرياضية بين المتغيرين س ، ص معادلاتها من الدرجة الثانية كما يلي :
أ س2+ ب ص2 + ج س + د ص+ هــ = صفر
لكل أ ، ب ، جـ ، د ,هـ∊ح, أ ≠ صفر , ب≠ صفر إطلاقاً . واشكال منحنياتها كما يلي :
|
|
|
|
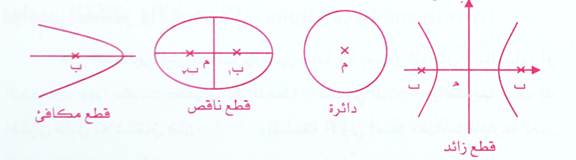
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
