The notation for four-vectors is different than it is for three-vectors. In the case of three-vectors, if we were to talk about the ordinary three-vector momentum we would write it p. If we wanted to be more specific, we could say it has three components which are, for the axes in question, p_x, p_y, and p_z, or we could simply refer to a general component as p_i, and say that i could either be x, y, or z, and that these are the three components; that is, imagine that i is any one of three directions, x, y, or z. The notation that we use for four-vectors is analogous to this: we write p_μ for the four-vector, and μ stands for the four possible directions t, x, y, or z.

We could, of course, use any notation we want; do not laugh at notations; invent them, they are powerful. In fact, mathematics is, to a large extent, invention of better notations. The whole idea of a four-vector, in fact, is an improvement in notation so that the transformations can be remembered easily. A_μ, then, is a general four-vector, but for the special case of momentum, the p_t is identified as the energy, p_x is the momentum in the x-direction, p_y is that in the y-direction, and p_z is that in the z-direction. To add four-vectors, we add the corresponding components.

If there is an equation among four-vectors, then the equation is true for each component. For instance, if the law of conservation of three-vector momentum is to be true in particle collisions, i.e., if the sum of the momenta for a large number of interacting or colliding particles is to be a constant, that must mean that the sums of all momenta in the x-direction, in the y-direction, and in the z-direction, for all the particles, must each be constant. This law alone would be impossible in relativity because it is incomplete; it is like talking about only two of the components of a three-vector. It is incomplete because if we rotate the axes, we mix the various components, so we must include all three components in our law. Thus, in relativity, we must complete the law of conservation of momentum by extending it to include the time component. This is absolutely necessary to go with the other three, or there cannot be relativistic invariance. The conservation of energy is the fourth equation which goes with the conservation of momentum to make a valid four-vector relationship in the geometry of space and time. Thus, the law of conservation of energy and momentum in four-dimensional notation is

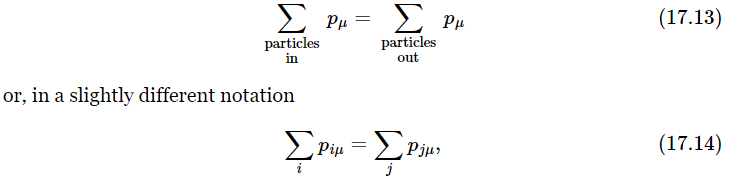
where i=1, 2, … refers to the particles going into the collision, j=1, 2, … refers to the particles coming out of the collision, and μ=x, y, z, or t. You say, “In which axes?” It makes no difference. The law is true for each component, using any axes.

In vector analysis we discussed one other thing, the dot product of two vectors. Let us now consider the corresponding thing in space-time. In ordinary rotation we discovered there was an unchanged quantity x²+y²+z². In four dimensions, we find that the corresponding quantity is t²−x²−y²−z² (Eq. 17.3). How can we write that? One way would be to write some kind of four-dimensional thing with a square dot between, like A_μ⊡B_μ; one of the notations which is actually used is

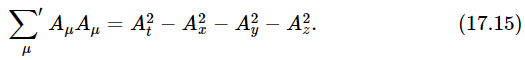
The prime on ∑ means that the first term, the “time” term, is positive, but the other three terms have minus signs. This quantity, then, will be the same in any coordinate system, and we may call it the square of the length of the four-vector. For instance, what is the square of the length of the four-vector momentum of a single particle? This will be equal to p²_t−p²_x−p²_y−p²_z or, in other words, E²−p², because we know that p_t is E. What is E²−p²? It must be something which is the same in every coordinate system. In particular, it must be the same for a coordinate system which is moving right along with the particle, in which the particle is standing still. If the particle is standing still, it would have no momentum. So in that coordinate system, it is purely its energy, which is the same as its rest mass. Thus E²−p²=m²₀. So we see that the square of the length of this vector, the four-vector momentum, is equal to m²₀.

From the square of a vector, we can go on to invent the “dot product,” or the product which is a scalar: if a_μ is one four-vector and b_μ is another four-vector, then the scalar product is

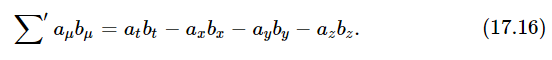
It is the same in all coordinate systems.

Finally, we shall mention certain things whose rest mass m₀ is zero. A photon of light, for example. A photon is like a particle, in that it carries an energy and a momentum. The energy of a photon is a certain constant, called Planck’s constant, times the frequency of the photon: E=hν. Such a photon also carries a momentum, and the momentum of a photon (or of any other particle, in fact) is h divided by the wavelength: p=h/λ. But, for a photon, there is a definite relationship between the frequency and the wavelength: ν=c/λ. (The number of waves per second, times the wavelength of each, is the distance that the light goes in one second, which, of course, is c.) Thus we see immediately that the energy of a photon must be the momentum times c, or if c=1, the energy and momentum are equal. That is to say, the rest mass is zero. Let us look at that again; that is quite curious. If it is a particle of zero rest mass, what happens when it stops? It never stops! It always goes at the speed c. The usual formula for energy is 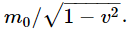 Now can we say that m₀=0 and v=1, so the energy is 0? We cannot say that it is zero; the photon really can (and does) have energy even though it has no rest mass, but this it possesses by perpetually going at the speed of light!

We also know that the momentum of any particle is equal to its total energy times its velocity: if c=1, p=vE or, in ordinary units, p=vE/c². For any particle moving at the speed of light, p=E if c=1. The formulas for the energy of a photon as seen from a moving system are, of course, given by Eq. (17.12), but for the momentum we must substitute the energy divided by c (or by 1 in this case). The different energies after transformation means that there are different frequencies. This is called the Doppler effect, and one can calculate it easily from Eq. (17.12), using also E=p and E=hν.

As Minkowski said, “Space of itself, and time of itself will sink into mere shadows, and only a kind of union between them shall survive.”