كان تصور طومسون للذرة يشبه إلى حد كبير تصور قطعة من الكعك منثورا عليها قطع من الزبيب تكون الكعكة ككل هي الشحنة الموجبة وقطع الزبيب هي الشحنات السالبة (الالكترونات). تحتوي الذرة على عدد Z من الالكترونات موزعة بشكل منتظم على الشحنة الموجبة والتي بدورها تحمل شحنة موجبة مستمرة تساوي (Ze) كما هو موضح بالشكل (1–2) حيث نلاحظ أن نصف قطر الذرة ككل هو R، ويوجد نصف قطر اخر r، وهذا السطح وهمي، يسمى بسطح جاوس Gauss's surface. وقد وضعناه حتى نستطيع حساب المجال الكهربائي ومن ثم حساب القوة المؤثرة على الإلكترون والذي يبعد مسافة r من مركز الكرة. تعطى تلك القوة بالعلاقة التالية ¹.

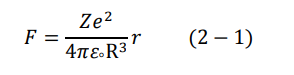
كان حجم الذرة معلوما في ذاك الوقت، فقد كان في حدود الانجستروم (m ^10–10)، وعلى أقرب تقدير في حدود (m ^10–100.1 * ) طالما أن حجم الذرة صغير الى هذا الحد، سيكون تأثير المجال الكهربائي للشحنة الكهربائية المستمرة صغير نسبيا، مما يجعل تأثيره على انحراف قذيفة خارجية مشحونة بشحنه موجبة صغير جدا.

تعود تلك الفكرة الرائعة الى الرائع رذرفورد. لقد وجد بهذه الفكرة الطريقة المناسبة للتأكد من صحة نموذج أستاذه طومسون، واقترح على طالبيه مارسدن وجايجر Marsden and Giger بالبدء في الاختبار العملي للتأكد من صحة نموذج طومسون.

استخدمت جسيمات ألفا أنوية الهيليوم، بروتونات ونيترونات كمقذوفات، ولما كانت كتلة أنوية الهيليوم كبيرة جدا بالنسبة للإلكترونات، فأنه بالإمكان إهمال قوة الجذب الكهربائي بينهما وبين الالكترونات المنتشرة فوق سطح الذرة على هيئة حبيبات. إذن لا يبقى سوى تأثير الشحنة الكهربائية الموجبة المنتشرة بشكل مستمر في الذرة.

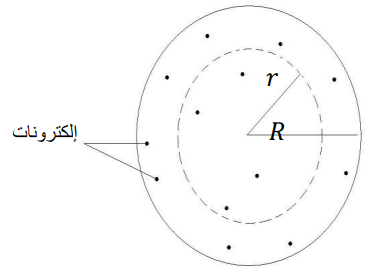
شكل (1–2)

نموذج طومسون الذري

يوضح الشكل (2-2) دخول جسيمة ألفا داخل مجال الذرة وتعرضها للانحراف بزاوية قدرها θ عن مسارها الأصلي. سوف نستخدم هنا الاحداثيات القطبية لتحديد موقع جسيمة ألفا داخل الذرة.

تدخل القذيفة داخل الذرة على ارتفاع b من المركز تسمى المسافة b بمعامل التصادم impact parameter الحساب الزاوية θ رياضيا، سنعتبر أن سرعة القذيفة أقل بكثير من سرعة الضوء (c >> v) وذلك لإهمال تأثير الميكانيكا النسبية تتلقى المقذوفة عند دخولها مجال الذرة قوة دفع تغير من قيمة قوة الدفع الأساسية في اتجاه y. تعطى تغير كمية الدفع بالعلاقة التالية ²:

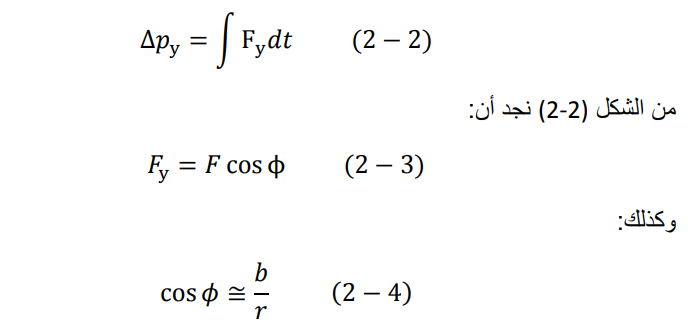
تمتلك المقذوفة (نواة الهيليوم) شحنة مقدارها ze، وبالتالي تكون القوة المؤثرة عليها حسب العلاقة (1-2) هي:

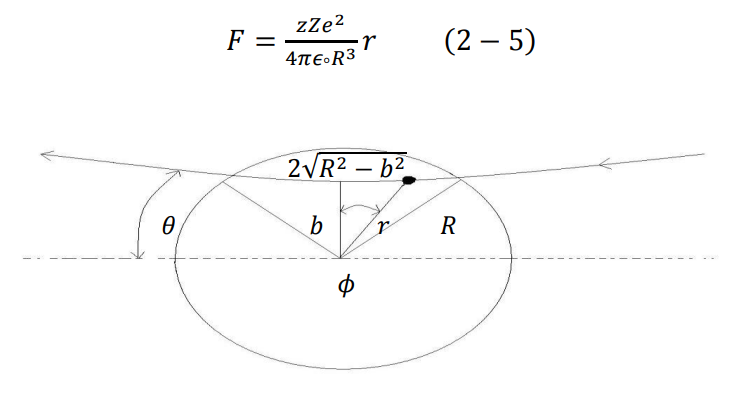
شكل (2-2)

انحراف جسيمة ألفا عند دخولها مجال ذرة طومسون، وذلك بسبب الشحنة الكهربائية الموجبة المنتشرة.

بتعويض المعادلات (3-2) و(4-2) و(5-2) في (2-2) نحصل على:

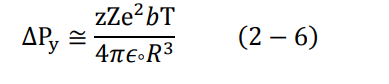
حيث T هو الوقت الكلي الذي تقطعه المقذوفة خلال مرورها داخل الذرة، ويساوي المسافة الكلية على السرعة. بحسب الشكل (2-2) يعطى كالتالي:

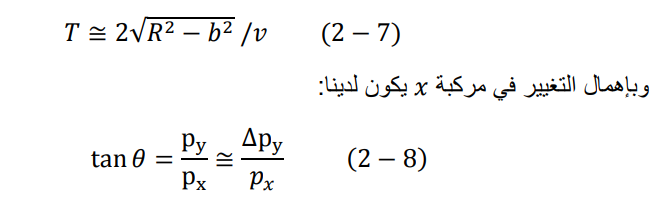
إذا كانت الزاوية θ صغيرة جدا، فأن θ ≈ θ tan. بتعويض العلاقة (7-2) في العلاقة (6-2) ومن ثم تعويض الناتج في العلاقة (8-2) نحصل على:

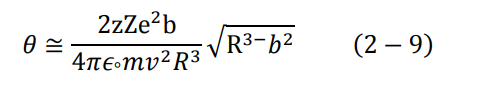
وهذه العلاقة هي التي تحسب انحراف القذيفة عند مرورها داخل الذرة نلاحظ اعتماد زاوية الانحراف θ على معامل التصادم b، لذلك لو كانت 0 = b تكون 0 = θ وهذا يعني أن القذيفة لن تنحرف أبدا لأن مجموع القوى المؤثرة عليها يساوي صفر عندما تكون b = R نجد مرة أخرى أن الناتج صفر، وبالتالي لا تنحرف القذيفة، وتعليل ذلك هو أن القوة تؤثر على المقذوفة فقط داخل الذرة، أي عندما (R > b).

في الواقع يصعب تجريبيا تحديد الزاوية θ بدقة. لذلك لا بد بأخذ قيمة متوسطة للزاوية θ، وسنرمز لها بالرمز θ_avg. حتى نحصل على هذه الزاوية سنضع 2/b = R كقيمة متوسطة. في هذه الحالة تصبح المعادلة (9-2) كالتالي:

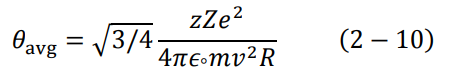
إن كل ما قمنا به في هذه المعالجة الرياضية كان على اعتبار قذف جسيمة ألفا واحدة فقط. لكن من المستحيل أن يتم ذلك تجريبيا، إذ لا نستطيع التحكم في عدد الجسيمات المقذوفة. إضافة إلى ذلك يصعب التحكم بمعامل التصادم b وهذا هو سبب اختيارنا لقيمة متوسطة للزاوية θ.

استخدم رذرفورد ومعاونوه في تجربة بعثرة جسيمات ألفا رقيقة من الذهب سمكها (m ^6–10). لو اعتبرنا أن نصف قطر الذرة هو R = 10^–10m، وطاقة حركة جسيمة ألفا تساوي k = 5 MeV مع 2 = z (نواة الهيليوم) و79 = Z (العدد الذري لذرة الذهب)، مع اعتبار mv² = 2k، سنحصل من المعادلة (10–2) على:

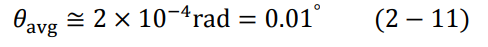
يوضح الشكل (3–2) تبعثر جسيمات ألفا خلال مرورها بصفيحة الذهب. طالما أن الصفيحة المستخدمة هي صفيحة ذهب، سوف تصطدم جسيمات ألفا بحوالي 10⁴ = N ذرة. ستكون انحرافات جسيمات ألفا مختلفة كما هو موضح بالشكل نفسه، وتكون القيمة المتوسطة لكل زاوية انحراف هي _avgθ. تعطى العلاقة بين θ و_avgθ كالتالي:

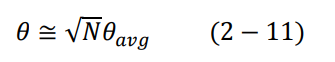
لم تكن نتائج بعثرة جسيمات ألفا بواسطة صفيحة من الذهب مؤيدة لنموذج طومسون بالمرة. كان من المتوقع أن تنحرف جسيمات ألفا بزوايا صغيرة بحدود 0.01º. ولكن لم يحدث ذلك، وجاءت النتائج مخالفة تماما لما هو متوقع، وكانت كالتالي:

1– معظم جسيمات ألفا نفذت دون أن تنحرف، وبعضها انحرفت بزوايا صغيرة، وعلى التقريب نقول بحدود 0.01º = θ.

2– عدد قليل من جسيمات ألفا انحرفت بزوايا كبيرة، ولكن أقل من 90º. أي _avgθ > θ > 90º.

3– عدد قليل جدا من جسيمات ألفا ارتدت إلى الوراء. أي °90 < θ.

بات واضحا الآن أن نتائج تجربة بعثرة جسيمات ألفا غير متوافقة تماما مع نموذج طومسون. فعلى الرغم من أن معظم جسيمات ألفا قد انحرفت بشكل صغير، إلا أن العدد القليل من الجسيمات المنحرفة بشكل كبير، والعدد القليل جدا من الجسيمات المرتدة إلى الخلف، كافي لنقض نموذج طومسون.

لقد رأى رذرفورد ومعانوه ضرورة تعديل كعكة طومسون. لذلك راح يبحث عن نموذج أخر يتفق تماما مع نتائج تجربته ولكي يجد ذلك النموذج لم يجد سوى حل واحد، وهو اختراع مجموعة شمسية ولكن على المستوى الذري.

___________________________________

هوامش

[1] من الممكن مشاهدة البرهان في كتب أساسيات الفيزياء، قسم الفيزياء الكهربائية.

[2] سوف نتبع في استنتاج المعادلة النهائية كتاب: Kenneth Krane، Modern Physics، John Wiely، 1996، P175 – 177