بادئ ذي بدء، لننظر في أمر التراجعات، وتحديدًا حالة المريخ. فبمعدل مرتين في العام تقريبًا، يبدو الكوكب الأحمر (الذي كان في نظر كوبرنيكوس ليس أكثر من نجم ذي لون يميل إلى الصفرة) وكأنه يتراجع للخلف في ظلام الليل، ثم يستأنف مساره عند ارتفاع أدنى من ذي قبل، حتى إن مساره عندئذ يشبه منحنى على شكل الحرف الإنجليزي S، كلٌّ من بدايته ونهايته مشدودة للغاية نحو الخارج. كيف يمكن تفسير ذلك؟ مسكين بطليموس، الذي – لتشبثه بالبساطة الزائفة لمركزية الأرض – استثمر علومه الرياضية في دائرة لامتراكزة يتحرك مركزها شرقًا حول مركز مسارات كسوفية عُينت خطأً وبسرعة تعادل سرعة الشمس المقدرة خطأ في دورانها حول الأرض، عندما يكون المريخ عند هذه الدائرة اللامتراكزة، يتحرك غربًا بسرعة تعادل سرعة المرور الزاوي، وإذا رسمنا خطا مستقيما باتجاه الدائرة اللامتراكزة ... من خلال عيوننا ... بحيث تصبح النسبة بين أحد نصفيها وأصغر القطعتين الدائريتين التي صنعتها عيوننا هي نفس النسبة التي بين سرعة الدائرة اللامتراكزة وسرعة النجم.» فإن النجم – ويقصد المريخ – سوف يبدو أحيانًا كما لو كان يتقهقر!

وماذا عن كوبرنيكوس؟ إنه يواصل في ثبات تبيانه لنا المجموعة الشمسية من وجهة نظر تعتمد على أرض ليست مركزا للكون، وهي تصف حالات التراجع الكوكبية بأنها عارضة وعشوائية مثلها مثل محطات حياة كوبرنيكوس نفسه؛ بادوفا، فيرارا، ليدزبارك، أولشتين، فرومبورك. إنه يذكرنا، تحديدًا، بأن علماء الهندسة السابقين عليه فسروا عمليات تراجع الكواكب بأنها تحدث فقط نتيجة لحركات تلك الكواكب بالنسبة للشمس، بينما هي في الحقيقة بسبب «تزيح للجرم السماوي نتيجة للدائرة الفلكية العظيمة للأرض» (التفسير الحديث الموجز لهذا الأمر أن المريخ يسير بسرعة أبطأ من سرعة الأرض حول الشمس، وبميل طفيف على المسار الكسوفي.) ويعلن كوبرنيكوس في نشوة المنتصر (وسوف أحذف البرهان الهندسي): «رأيي أنه عندما يكون الكوكب عند النقطة «و»، فإنه يبدو لنا في صورة توقف عن الحركة؛ وأنه أيا كان حجم القوس الذي نأخذه على أي من جانبي النقطة «و»، فسوف نجد الكوكب يتقدم للأمام، إذا أخذنا القوس في اتجاه نقطة الأوج، ويتراجع للخلف، إذا كان القوس في اتجاه نقطة الحضيض.»

لم يكن هناك داعٍ لكي يبني نظريته الجديدة في حركة الكواكب من الصفر؛ إذ إن الحسابات الهندسية التي أجراها بطليموس، وكان الهدف منها التوافق مع المشاهدات، عبرت بالفعل عن علاقات رياضية حقيقية؛ ففي حاشية سفلية طويلة، يعتبر مترجم كتاب «المجسطي» هذه النظرية الخاصة بالتراجعات «معادلة تقريبًا لنظرية التحويل التي ينتقل بها المرء من النظرية البطلمية إلى النظرية الكوبرنيكية للكواكب الخارجية. إن نسبة نصف قطر الدائرة التي يتحرك عليها مركز الدائرة اللامتراكزة وصولًا إلى نصف قطر الدائرة اللامتراكزة» لدى بطليموس «هي ذاتها نسبة نصف قطر فلك التدوير إلى نصف قطر «المؤجِّل» في نظرية فلك التدوير لكوبرنيكوس. يكفينا أن نعيد القول

بإيجاز، حسبما هو مفهوم بديهيا، أن مركز الدائرة اللامتراكزة لدى بطليموس يقابل متوسط موقع الشمس لدى كوبرنيكوس.

وهكذا اقترب بنا كتاب «عن دورات الأجرام السماوية» من فهم حقيقة المدار المريخي. الآن، أين المريخ؟ في معرض مناقشتنا لمدار الزهرة طرحنا هذا السؤال من زاوية أكثر تعميما بكثير: ما الترتيب الذي من المفترض أن نضع فيه فلك الزهرة الكروي؟ أما وقد أجبنا عن هذه المسألة، فإننا نود الآن أن نتمكن من تحديد موضع إحداثيات كل كوكب في أي توقيت.

سوف تكون الخطوة الأولى تحديد فترات الكواكب.

يقول كوبرنيكوس – وهو محق في قوله – إن «الموضع الحقيقي لزحل والمشتري والمريخ لا يصبح مرئيا لنا إلا» أثناء المواجهة، التي، من المنطقي تمامًا، أن تحدث «في منتصف حالات تراجعها؛ إذ إنه عند ذلك التوقيت يقع ثلاثتها على خط مستقيم مع متوسط موضع الشمس، وتنحي جانبًا تزيحها.» (حسبما أخبرنا هو من قبل، لا يمكن مشاهدة الكواكب الداخلية في تلك الأوقات، ولهذا فإنه يقيس زواياها الخاصة بأقصى استطالة غربا وشرقا، ثم يحسب المتوسط بينها.)

في حالة زحل والمشتري والمريخ يعقد مقارنة بين «حالات الرصد الحديثة» الثلاث – رصده هو – مع ثلاث حالات رصد قديمة، ومن ثم يحدد مقدار ما يستغرقه كل كوكب في الدوران من موضع معين بين الشمس ونجم ثابت محدد عودة إلى نفس الموضع من جديد. وهو يطلق على هذه الحركة «دورة تزيح واحدة». سوف تتيح له تلك البيانات حساب المسافات الكوكبية على نحو أفضل مما فعل أي ممن سبقوه. وبتعبيره هو: «دعونا نتغاض في صمت عن كمّ الحسابات وتعقيدها ومللها.»

ثمة فكرة أخرى؛ وهي أن نعلّق على تلك الحسابات.

يبدأ شرح فلكي مبني على معارف عصرنا الحالي الذي ليست فيه الأرض مركزا للكون (عمر النص خمسون عامًا فقط) بالكلمات التالية: «الإجراء القياسي المتضمن هنا يتكون من دراسة حركة جسم ما في المجموعة الشمسية، مشكلا تقويمًا فلكيا يقوم على نظرية الجاذبية وعاقدًا مقارنةً بين التقويم الفلكي وبين ما يشاهد في عمليات الرصد.»

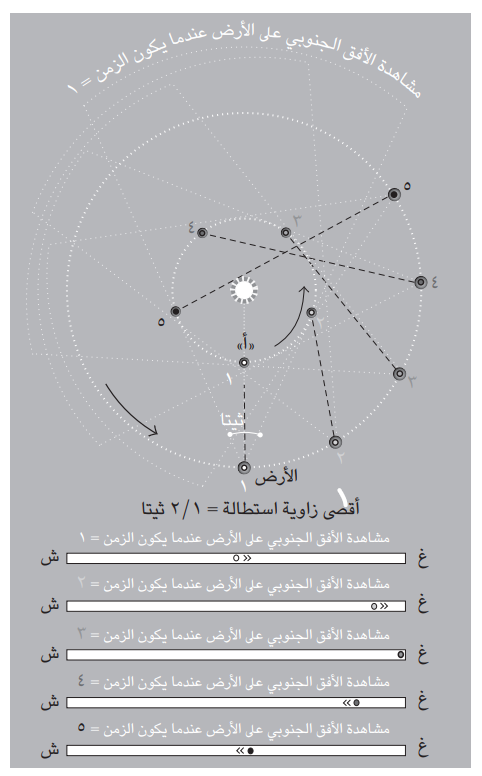
شكل 1: الحركة القهقرية الظاهرية لكوكب داخلي «أ» (منظر كوبرنيكي مبسط)

لكل فاصل زمني، أدر اشكل وتخيل انك تشاهد الأفق مقارنة بالزمن «1»، والأرض ند المركز السفلي.

الموضع الظاهري، واتجاه سير وسرعة «أ» حسب مسقطه على أفقنا (مفترضين أن باستطاعتنا دوما مشاهدته):

في هذا الشكل المعمم، ثمة مبالغة في السرعة النسبية للكوكب الداخلي، وحركته الظاهرية جرى تبسيطها (بطبيعة الحال الظواهر أكثر تعقيدًا من ذلك). تأمل المسار الظاهري للزهرة وكأنه يشاهد من الأرض في مسار الدائرتين الظاهرتين من حولنا، اللتين ليست علاماتهما النقطية الثلاث واحدة على الإطلاق نفذ كوكب الزهرة عملية تقهقر واحدة (الحلقة الموجودة عند R).

بافتراض وجود حركة دائرية منتظمة باتجاه عكس عقارب الساعة لكلٌّ من الكوكبين الأرض و«أ»، وكذلك بافتراض أن الكوكب «أ» يسير بسرعة أكبر من سرعة كوكبنا، لو كان «أ» والأرض عند الاقتران السفلي بعد مرور الزمن 1، سوف يُشاهد الكوكب «أ» في منتصف أفقنا. ثم إنه سوف ينجذب أبعد وأبعد باتجاه الغرب. وحسب ملاحظة كوبرنيكوس، فإنه سوف يتحرك باتجاه الغرب في بطء نسبي؛ حيث إن كلا الكوكبين يتحركان في نفس الاتجاه، حتى إن بعضًا من الحركة المحسوسة للكوكب «أ» تلغى بفعل حركة الأرض.

عند الزمن 3 يكون الكوكب «أ» قد تحرك إلى أبعد مدى غربًا يمكنه الوصول إليه فوق أفقنا؛ إذ إنه يكون قد أشرف على بلوغ أقصى بعد زاوي له.

عند الزمن 4 والزمن 5 يكون الكوكب «أ» قد بلغ بالفعل الجانب البعيد من الشمس. من وجهة نظرنا أنه يتحرك الآن باتجاه الشرق. لما كانت الأرض لا تزال تتحرك في نفس اتجاهها السابق، فإن سرعة الكوكب «أ» الظاهرية عبر أفقنا تزداد.

كان لكوبرنيكوس تقويمه الفلكي، وهو أُعدَّ تقويم من قبل بجهود بطليموس وهيبارخوس وغيرهما من المنكرين لذواتهم، ولكن رجاءً، ذكر نفسك من جديد أنه حتى نهاية أيامه سوف تظل نظرية الجاذبية غائبة عنه، التي كانت وظيفتها أن تمنح الكوكب المعني «حركته المتمركزة حول الشمس، التي تتحدد عن طريق عناصر مدارية وكتل تابعة من الكواكب المضطربة الحركة.» رجاءً تذكَّر هذا الكاهن المعتزل داخل برجه في فرومبورك، يعمل في دأب وصبر لاستكشاف الدوائر الكوكبية وأوضاعها، ويفعل ذلك دون ما نعتبره الآن أدوات لا غنى عنها تعتمد على قوانين نيوتن الميكانيكية. لهذا السبب تتعاظم حلوله الهندسية لتتشعب وتتشابك لتصبح أشبه بالزهرة النجمية العنكبوتية المصنوعة من خطوط منقوشة في صحون الكنائس البولندية؛ ومع ذلك فهو لم ينته بعد.

ويواصل فلكيو قرننا العشرين حديثهم بالقول: «وتتعقد المشكلة بسبب أن عمليات الرصد تتم من مرصد موجود فوق سطح الأرض؛ ومن ثم يُدخِل حساب التقويم الفلكي المتمركز حول الأرض الحركة الفلكية لكوكب الأرض حول الشمس في المسألة ... ويجب السماح بإدخال عنصر التفاوت القمري الذي يحدث بسبب حركة مركز الأرض حول مركز كتلة منظومة الأرض – القمر. هذا المدار عبارة عن انعكاس مصفّر لحركة القمر حول الأرض.» ومن جديد لن يكون لدى كوبرنيكوس مطلقًا أي فرصة للسماح بالتفاوت القمري بدخول المعادلة؛ حيث إنه لا يملك أي نظرية للجاذبية تبين له وجوده وأهميته.

بوضع تلك الصعوبات الجمة في الاعتبار، فإنه مما يستحق الملاحظة الشديدة أن أنصاف أقطار المؤجلات التي يحسبها كوبرنيكوس للكواكب، والتي تترجم إلى متوسطات أنصاف أقطار مداراتها الفعلية التي على شكل قطع ناقص، سوف تكون قريبة من الدقة في حالتي عطارد وزحل، الكوكبين الطرفيين من الكواكب المعلومة وقتئذ (وهنا يتجاوز خطوه نسبة 3 في المائة)؛ وفي حالة الزهرة والمريخ والمشتري، سوف يكون خطوه بنسبة 0.55 في المائة أو أقل.

«كما يجب علاوة على ذلك السماح بوضع حقيقة أن الراصد يتحرك حول محور دوران الأرض في الاعتبار. ويتم ذلك عن طريق تطبيق تصويب التزيح القائم على مركزية الأرض بالنسبة للوضع المرصود، ومن ثم اختزاله إلى وضع قائم على مركزية الأرض. ويتطلب هذا التصويب إدخال التزيح الشمسي في المسألة، ويمكن إجراؤه إذا كان بعد الجسم المرصود المعبر عنه بالوحدات الفلكية، معلومًا بدرجة كافية.»

هذا الأمر في مقدور كوبرنيكوس أن يفعله، ولكن هذا يُعزى فقط إلى أنه حسب هذا «البعد بالوحدات الفلكية» بطريقته الخاصة: مدارات ذات شكل غير صحيح حول نقطة غير صحيحة، والكل دعمه سوء فهم أرسطي للحركة! ومن ثم يقيم الفلكي زدنيك كوبول كوبرنيكوس قائلًا إنه بذل جهدًا شاقًا دون أن يكلل بكثير من النجاح.»

تخيل كوبرنيكوس خلال الساعات القليلة لليل البولندي، يراقب من خلال أسطرلابه. «علاوة على ذلك، أجرينا عمليات رصد لاقتران المريخ بأول نجم لامع في المجموعة المخلبية، ويسمى المخلب الجنوبي ...» وبرسم دائرة لامتراكزة يخترقها سهم «أ ب جـ» ترتبط بالفلك التدويري «ب و» بمثلثين ذوي استطالة يحدد كوبرنيكوس متوسط الدائرة الفلكية للمريخ.

يقول كوبرنيكوس في أحد المواضع: «عقدنا مقارنة بين تلك الحالات الثلاث للرصد التي أجراها بطليموس للمريخ وثلاث عمليات رصد أخرى، لم نهمل في إجرائها.» وفي موضع آخر يحسب زاوية القمر «ق» والأرض «أ» والمريخ «م»، «ق أ م»، ليجدها 50’ 47°، «ومن هنا فإن حركة الكوكب بداية من المواجهة الشمسية الأولى حتى الثانية ظاهرة والرقم متفق مع التجارب السابقة» في إيجاز، يحدد كوبرنيكوس السنوات التي مرت بين المواجهتين، ويحول الزمن إلى درجات على دائرة بأسلوبه المعهود، ثم يضع إحداثيات الموقع لكل كوكب على كرة النجوم الثابتة، وبعدها يرسم دوائره. «القوس المعروف «أ ب» يقع قبالة الزاوية غير معلومة المقدار «أ و ب» ...» وهو يحدد حاليًّا متوسط التزيح لكل كوكب. في حالة المريخ، يذكر كتاب «عن دورات الأجرام السماوية»، اعتمادًا على عمليات رصد أجراها هيبارخوس وبطليموس، حدوث 37 «دورة تزيح» خلال زمن يزيد قليلا على 79 سنة شمسية؛ بما يعني أن الأرض تمر بالمريخ 37 مرة خلال تلك الفترة، وخلالها أيضًا «يكمل الكوكب في حركته الخاصة 42 فترة مضافًا إليها درجتان و24 دقيقة و56 ثانية.» من تلك البيانات، يشتق كوبرنيكوس (يحذف التفاصيل، كما هي العادة، لكنني أفترض أنه أجرى عملية قسمة 79 على 37، ثم ضرب الناتج في 365) دائرة واحدة للتزيح المريخي ليكون الناتج 779 يومًا.

نحن الآن نحسب الفترة المدارية للمريخ فنجدها 1.88 عامًا، أو 686 يومًا. والقيمة التي توصل إليها كوبرنيكوس لـ 42 فترة خلال 79 عامًا ناتجها 1.88، وهو ما يؤكد إعجابي بالراصدين القدماء، ولكوبرنيكوس كان في استطاعة بطليموس أن يجري تلك العملية الحسابية البسيطة فقط لو أنه افترض مركزية الشمس أولًا.

هناك عملية حسابية أخرى يمكن إجراؤها باستخدام رقم دورات التزيح المريخي تعزز ما توصلنا إليه لتوّنا؛ إذ لو كانت الأرض تمر بالمريخ 37 مرة خلال نفس المقدار الزمني الذي يدور فيه المريخ حول الشمس 42 مرة، فلا بد لنا أن نتوقع أن الفترة المريخية 1 و3742 من السنوات الشمسية، وهو ما يعطينا من جديد الرقم 1.88 سنة.

«زد على ذلك، أننا أجرينا عمليات الرصد على الاقتران بين المريخ وأول نجم لامع من المجموعة المخلبية، ويسمى المخلب الجنوبي ...» فبرسم دائرة لامتراكزة يخترقها سهم «أ ب جـ» ترتبط بالفلك التدويري «ب و» بمثلثين ذوي استطالة، يحدد كوبرنيكوس متوسط الدائرة الفلكية للمريخ فيجده مساويًا لنصف قطر المسار الكسوفي مضافًا إليه 11’’ 31’.

القيمة المعاصرة لمدار المريخ تحدد متوسط نصف قطر يبلغ 1.524 وحدة فلكية، أو مرة ونصف قدر نصف قطر المسار الكسوفي. وبقسمة الدقائق الإحدى والثلاثين التي توصل إليها كوبرنيكوس على 60 يكون الناتج 0.516؛ فإذا أضفنا تلك القيمة لوحدة نصف قطر كسوفي واحدة أو وحدة فلكية واحدة، نحصل على رقم قريب جدًّا من الواقع وهو 1.516، وجميع تلك الحسابات أجريت باستخدام دوائر وزوايا مأخوذة من عمليات رصد قديمة! «كذلك الحال أيضًا مع المريخ؛ فالحركات والمقادير والمسافات جرى تحليلها منطقيًّا إلى نسبة ثابتة بواسطة حركة الأرض.»