Königsberg Bridge Problem

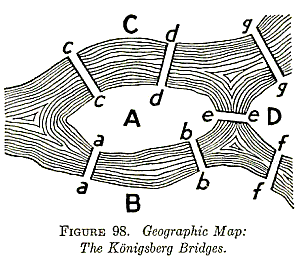
The Königsberg bridge problem asks if the seven bridges of the city of Königsberg (left figure; Kraitchik 1942), formerly in Germany but now known as Kaliningrad and part of Russia, over the river Preger can all be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began. This is equivalent to asking if the multigraph on four nodes and seven edges (right figure) has an Eulerian cycle. This problem was answered in the negative by Euler (1736), and represented the beginning of graph theory.

On a practical note, J. Kåhre observes that bridges  and  no longer exist and that  and  are now a single bridge passing above  with a stairway in the middle leading down to . Even so, there is still no Eulerian cycle on the nodes , , , and  using the modern Königsberg bridges, although there is an Eulerian path (right figure). An example Eulerian path is illustrated in the right figure above where, as a last step, the stairs from  to  can be climbed to cover not only all bridges but all steps as well.

REFERENCES

Biggs, N. L.; Lloyd, E. K.; and Wilson, R. J. Graph Theory 1736-1936. Oxford, England: Oxford University Press, 1976.

Bogomolny, A. "Graphs." http://www.cut-the-knot.org/do_you_know/graphs.shtml.Chartrand, G. "The Königsberg Bridge Problem: An Introduction to Eulerian Graphs." §3.1 in Introductory Graph Theory. New York: Dover, pp. 51-66, 1985.

Euler, L. "Solutio problematis ad geometriam situs pertinentis." Comment. Acad. Sci. U. Petrop. 8, 128-140, 1736.

Reprinted in Opera Omnia Series Prima, Vol. 7. pp. 1-10, 1766.

Harary, F. Graph Theory. Reading, MA: Addison-Wesley, pp. 1-2, 1994.Kåhre, J. "K:)nigsberg Bridges Solved." http://www.matheory.info/konigsberg/.Kraitchik, M. §8.4.1 in Mathematical Recreations. New York: W. W. Norton, pp. 209-211, 1942.

Newman, J. "Leonhard Euler and the Königsberg Bridges." Sci. Amer. 189, 66-70, 1953.

Pappas, T. "Königsberg Bridge Problem & Topology." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 124-125, 1989.

Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 192, 1990.

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 256-259, 1999.Wilson, R. J. "An Eulerian Trail through Königsberg." J. Graph Th. 10, 265-275, 1986.