von Neumann-Bernays-Gödel Set Theory

von Neumann-Bernays-Gödel set theory (abbreviated "NBG") is a version of set theory which was designed to give the same results as Zermelo-Fraenkel set theory, but in a more logically elegant fashion. It can be viewed as a conservative extension of Zermelo-Fraenkel set theory in the sense that a statement about sets is provable in NBG if and only if it is provable in Zermelo-Fraenkel set theory.

Zermelo-Fraenkel set theory is not finitely axiomatized. For example, the axiom of replacement is not really a single axiom, but an infinite family of axioms, since it is preceded by the stipulation that it is true "for any set-theoretic formula 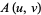." Montague (1961) proved that Zermelo-Fraenkel set theory is not finitely axiomatizable, i.e., there is no finite set of axioms which is logically equivalent to the infinite set of Zermelo-Fraenkel axioms. In contrast, von Neumann-Bernays-Gödel set theory has only finitely many axioms, and this was the main motivation in its construction. This was accomplished by extending the language of Zermelo-Fraenkel set theory to be capable of talking about set classes.

REFERENCES:

Itô, K. (Ed.). "Bernays-Gödel Set Theory." §33C in Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 1. Cambridge, MA: MIT Press, p. 148, 1986.

Mendelson, E. Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.

Montague, R. "Semantic Closure and Non-Finite Axiomatizability. I." In Infinitistic Methods, Proceedings of the Symposium on Foundations of Mathematics, (Warsaw, 2-9 September 1959). Oxford, England: Pergamon, pp. 45-69, 1961.