Bessel's Finite Difference Formula

An interpolation formula, sometimes known as the Newton-Bessel formula, given by

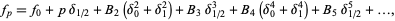(1)

for , where 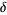 is the central difference and

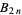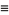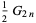			(2)
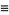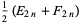			(3)
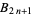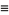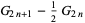			(4)
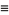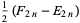			(5)
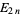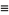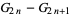			(6)
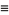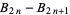			(7)
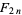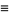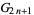			(8)
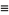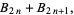			(9)

where 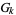 are the coefficients from Gauss's backward formula and Gauss's forward formula 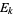and  and 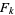 are the coefficients from Everett's formula. The 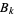s also satisfy

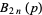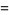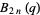			(10)
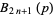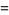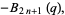			(11)

for

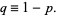(12)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 880, 1972.

Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., pp. 90-91, 1990.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 433, 1987.

Whittaker, E. T. and Robinson, G. "The Newton-Bessel Formula." §24 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 39-40, 1967.