


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-8-2021
Date: 29-9-2021
Date: 30-8-2021
|
The Lagrange interpolating polynomial is the polynomial 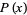 of degree
of degree 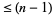 that passes through the
that passes through the 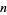 points
points 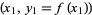 ,
, 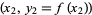 , ...,
, ..., 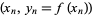 , and is given by
, and is given by
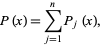 |
(1) |
where
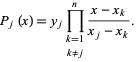 |
(2) |
Written explicitly,
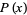 |
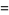 |
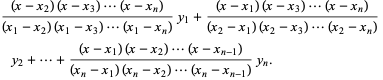 |
(3) |
The formula was first published by Waring (1779), rediscovered by Euler in 1783, and published by Lagrange in 1795 (Jeffreys and Jeffreys 1988).
Lagrange interpolating polynomials are implemented in the Wolfram Language as InterpolatingPolynomial[data, var]. They are used, for example, in the construction of Newton-Cotes formulas.
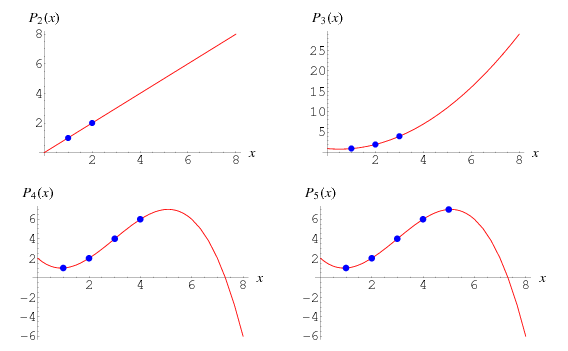
When constructing interpolating polynomials, there is a tradeoff between having a better fit and having a smooth well-behaved fitting function. The more data points that are used in the interpolation, the higher the degree of the resulting polynomial, and therefore the greater oscillation it will exhibit between the data points. Therefore, a high-degree interpolation may be a poor predictor of the function between points, although the accuracy at the data points will be "perfect."
For 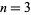 points,
points,
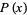 |
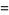 |
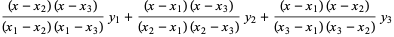 |
(4) |
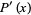 |
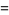 |
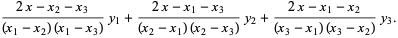 |
(5) |
Note that the function 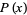 passes through the points
passes through the points 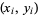 , as can be seen for the case
, as can be seen for the case 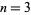 ,
,
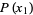 |
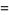 |
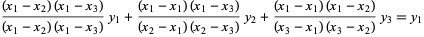 |
(6) |
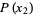 |
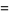 |
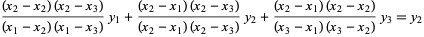 |
(7) |
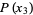 |
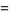 |
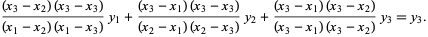 |
(8) |
Generalizing to arbitrary 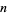 ,
,
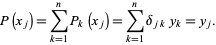 |
(9) |
The Lagrange interpolating polynomials can also be written using what Szegö (1975) called Lagrange's fundamental interpolating polynomials. Let
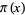 |
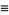 |
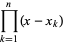 |
(10) |
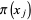 |
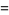 |
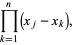 |
(11) |
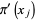 |
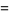 |
![[(dpi)/(dx)]_(x=x_j)](https://mathworld.wolfram.com/images/equations/LagrangeInterpolatingPolynomial/Inline38.gif) |
(12) |
 |
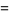 |
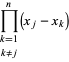 |
(13) |
so that 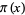 is an
is an 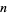 th degree polynomial with zeros at
th degree polynomial with zeros at 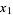 , ...,
, ..., 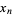 . Then define the fundamental polynomials by
. Then define the fundamental polynomials by
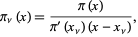 |
(14) |
which satisfy
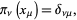 |
(15) |
where 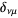 is the Kronecker delta. Now let
is the Kronecker delta. Now let 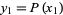 , ...,
, ..., 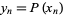 , then the expansion
, then the expansion
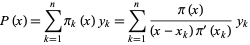 |
(16) |
gives the unique Lagrange interpolating polynomial assuming the values 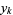 at
at 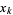 . More generally, let
. More generally, let 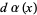 be an arbitrary distribution on the interval
be an arbitrary distribution on the interval ![[a,b]](https://mathworld.wolfram.com/images/equations/LagrangeInterpolatingPolynomial/Inline52.gif) ,
, 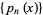 the associated orthogonal polynomials, and
the associated orthogonal polynomials, and 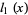 , ...,
, ..., 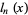 the fundamental polynomials corresponding to the set of zeros of a polynomial
the fundamental polynomials corresponding to the set of zeros of a polynomial 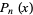 . Then
. Then
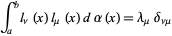 |
(17) |
for 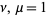 , 2, ...,
, 2, ..., 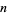 , where
, where 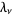 are Christoffel numbers.
are Christoffel numbers.
Lagrange interpolating polynomials give no error estimate. A more conceptually straightforward method for calculating them is Neville's algorithm.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 878-879 and 883, 1972.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 439, 1987.
Jeffreys, H. and Jeffreys, B. S. "Lagrange's Interpolation Formula." §9.011 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 260, 1988.
Pearson, K. Tracts for Computers 2, 1920.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Polynomial Interpolation and Extrapolation" and "Coefficients of the Interpolating Polynomial." §3.1 and 3.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 102-104 and 113-116, 1992.
Séroul, R. "Lagrange Interpolation." §10.9 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 269-273, 2000.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 329 and 332, 1975.
Waring, E. Philos. Trans. 69, 59-67, 1779.
Whittaker, E. T. and Robinson, G. "Lagrange's Formula of Interpolation." §17 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 28-30, 1967.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|