


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-9-2021
Date: 13-10-2021
Date: 16-2-2016
|

The circle map is a one-dimensional map which maps a circle onto itself
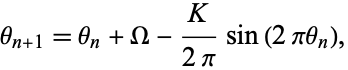 |
(1) |
where 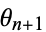 is computed mod 1 and
is computed mod 1 and 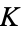 is a constant. Note that the circle map has two parameters:
is a constant. Note that the circle map has two parameters: 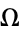 and
and 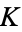 .
. 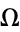 can be interpreted as an externally applied frequency, and
can be interpreted as an externally applied frequency, and 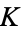 as a strength of nonlinearity. The circle map exhibits very unexpected behavior as a function of parameters, as illustrated above.
as a strength of nonlinearity. The circle map exhibits very unexpected behavior as a function of parameters, as illustrated above.
It is related to the standard map
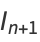 |
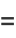 |
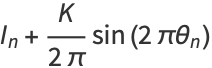 |
(2) |
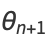 |
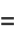 |
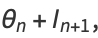 |
(3) |
for  and
and  computed mod 1. Writing
computed mod 1. Writing  as
as
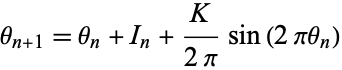 |
(4) |
gives the circle map with 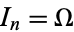 and
and 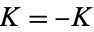 .
.
The one-dimensional Jacobian of the circle map is
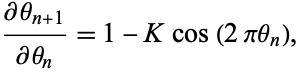 |
(5) |
so the circle map is not area-preserving.
The unperturbed circle map has the form
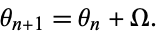 |
(6) |
If 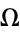 is rational, then it is known as the map map winding number, defined by
is rational, then it is known as the map map winding number, defined by
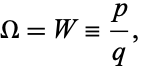 |
(7) |
and implies a periodic trajectory, since 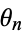 will return to the same point (at most) every
will return to the same point (at most) every 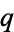 map orbits. If
map orbits. If 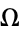 is irrational, then the motion is quasiperiodic. If
is irrational, then the motion is quasiperiodic. If 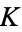 is nonzero, then the motion may be periodic in some finite region surrounding each rational
is nonzero, then the motion may be periodic in some finite region surrounding each rational 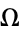 . This execution of periodic motion in response to an irrational forcing is known as mode locking.
. This execution of periodic motion in response to an irrational forcing is known as mode locking.
If a plot is made of 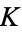 vs.
vs.  with the regions of periodic mode-locked parameter space plotted around rational
with the regions of periodic mode-locked parameter space plotted around rational  values (map winding numbers), then the regions are seen to widen upward from 0 at
values (map winding numbers), then the regions are seen to widen upward from 0 at 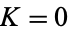 to some finite width at
to some finite width at 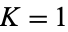 . The region surrounding each rational number is known as an Arnold tongue. At
. The region surrounding each rational number is known as an Arnold tongue. At 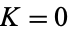 , the Arnold tongues are an isolated set of measure zero. At
, the Arnold tongues are an isolated set of measure zero. At 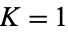 , they form a Cantor set of dimension
, they form a Cantor set of dimension 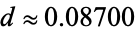 . For
. For 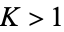 , the tongues overlap, and the circle map becomes noninvertible.
, the tongues overlap, and the circle map becomes noninvertible.
Let 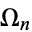 be the parameter value of the circle map for a cycle with map winding number
be the parameter value of the circle map for a cycle with map winding number  passing with an angle
passing with an angle  , where
, where 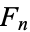 is a Fibonacci number. Then the parameter values
is a Fibonacci number. Then the parameter values 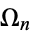 accumulate at the rate
accumulate at the rate
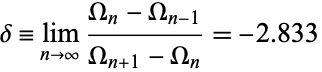 |
(8) |
(Feigenbaum et al. 1982).
REFERENCES:
Devaney, R. L. An Introduction to Chaotic Dynamical Systems. Redwood City, CA: Addison-Wesley, pp. 108-111, 1987.
Feigenbaum, M. J.; Kadanoff, L. P.; and Shenker, S. J. "Quasiperiodicity in Dissipative Systems: A Renormalization Group Analysis." Physica D 5, 370-386, 1982.
Rasband, S. N. "The Circle Map and the Devil's Staircase." §6.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 128-132, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|