
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-10-2021
Date: 21-11-2021
Date: 11-10-2021
|
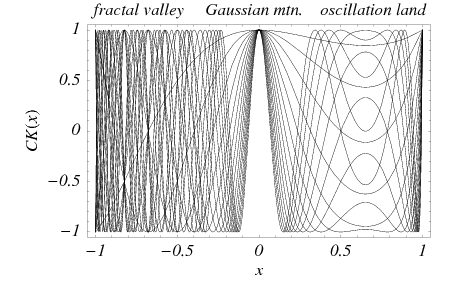
A fractal-like structure is produced for 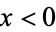 by superposing plots of Carotid-Kundalini functions
by superposing plots of Carotid-Kundalini functions 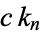 of different orders
of different orders 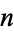 . the region
. the region 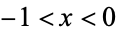 is called fractal land by Pickover (1995), the central region the Gaussian mountain range, and the region
is called fractal land by Pickover (1995), the central region the Gaussian mountain range, and the region 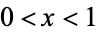 oscillation land. The plot above shows
oscillation land. The plot above shows 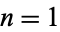 to 25. Gaps in fractal land occur whenever
to 25. Gaps in fractal land occur whenever
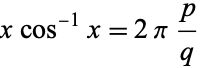 |
for 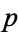 and
and 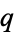 relatively prime integers. At such points
relatively prime integers. At such points 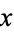 , the functions assume the
, the functions assume the ![[(q+1)/2]](https://mathworld.wolfram.com/images/equations/Carotid-KundaliniFractal/Inline10.gif) values
values 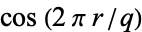 for
for 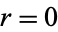 , 1, ...,
, 1, ..., 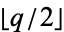 , where
, where ![[z]](https://mathworld.wolfram.com/images/equations/Carotid-KundaliniFractal/Inline14.gif) is the ceiling function and
is the ceiling function and 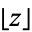 is the floor function.
is the floor function.
REFERENCES:
Pickover, C. A. "Are Infinite Carotid-Kundalini Functions Fractal?" Ch. 24 in Keys to Infinity. New York: Wiley, pp. 179-181, 1995.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|