


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-7-2021
Date: 22-6-2021
Date: 7-6-2021
|
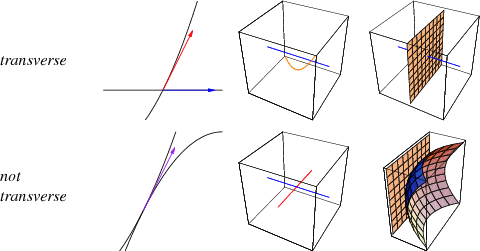
Two submanifolds  and
and  in an ambient space
in an ambient space  intersect transversally if, for all
intersect transversally if, for all 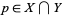 ,
,
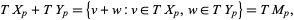 |
where the addition is in 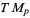 , and
, and 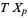 denotes the tangent map of
denotes the tangent map of 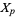 . If two submanifolds do not intersect, then they are automatically transversal. For example, two curves in
. If two submanifolds do not intersect, then they are automatically transversal. For example, two curves in  are transversal only if they do not intersect at all. When
are transversal only if they do not intersect at all. When 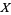 and
and 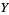 meet transversally then
meet transversally then 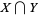 is a smooth submanifold of the expected dimension
is a smooth submanifold of the expected dimension 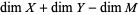 .
.
In some sense, two submanifolds "ought" to intersect transversally and, by Sard's theorem, any intersection can be perturbed to be transversal. Intersection in homology only makes sense because an intersection can be made to be transversal.
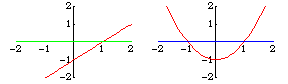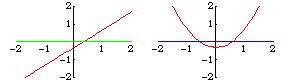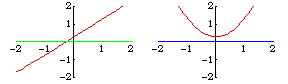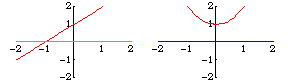
Transversality is a sufficient condition for an intersection to be stable after a perturbation. For example, the lines 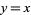 and
and 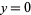 intersect transversally, as do the perturbed lines
intersect transversally, as do the perturbed lines 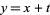 , and they intersect at only one point. However,
, and they intersect at only one point. However, 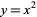 does not intersect
does not intersect 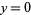 transversally. It intersects in one point, while
transversally. It intersects in one point, while 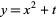 intersects in either none or two points, depending on whether
intersects in either none or two points, depending on whether 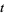 is positive or negative.
is positive or negative.
When 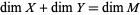 , then a transversal intersection is an isolated point. If the three spaces have an vector space orientation, then the transversal condition means it is possible to assign a sign to the intersection. If
, then a transversal intersection is an isolated point. If the three spaces have an vector space orientation, then the transversal condition means it is possible to assign a sign to the intersection. If 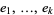 are an oriented basis for
are an oriented basis for 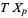 and
and 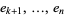 are an oriented basis for
are an oriented basis for 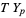 , then the intersection is
, then the intersection is 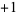 if
if 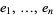 is oriented in
is oriented in 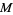 and
and 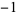 otherwise.
otherwise.
More generally, two smooth maps 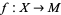 and
and 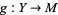 are transversal if whenever
are transversal if whenever 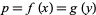 then
then 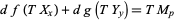 .
.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|