Harmonic Map

A map 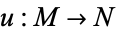, between two compact Riemannian manifolds, is a harmonic map if it is a critical point for the energy functional

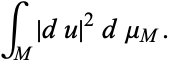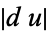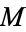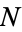The norm of the differential  is given by the metric on  and  and 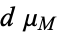 is the measure on 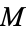. Typically, the class of allowable maps lie in a fixed homotopy class of maps.

The Euler-Lagrange differential equation for the energy functional is a non-linear elliptic partial differential equation. For example, when 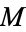 is the circle, then the Euler-Lagrange equation is the same as the geodesic equation. Hence,  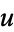is a closed geodesic iff  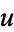is harmonic. The map from the circle to the equator of the standard 2-sphere is a harmonic map, and so are the maps that take the circle and map it around the equator  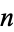times, for any integer 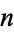. Note that these all lie in the same homotopy class. A higher-dimensional example is a meromorphic function on a compact Riemann surface, which is a harmonic map to the Riemann sphere.

A harmonic map may not always exist in a homotopy class, and if it does it may not be unique. When 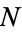 is negatively curved, a harmonic representative exists for each homotopy class, and is also unique. For surfaces, the harmonic maps have been classified, and are precisely the holomorphic maps and the anti-holomorphic maps. Thus by Hodge's theorem for surfaces, there are no non-trivial harmonic maps from the sphere to the torus.

A harmonic map between Riemannian manifolds can be viewed as a generalization of a geodesic when the domain dimension is one, or of a harmonic function when the range is a Euclidean space.