


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-5-2021
Date: 8-5-2021
Date: 28-6-2021
|
A principal bundle is a special case of a fiber bundle where the fiber is a group 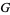 . More specifically,
. More specifically, 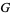 is usually a Lie group. A principal bundle is a total space
is usually a Lie group. A principal bundle is a total space 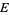 along with a surjective map
along with a surjective map 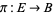 to a base manifold
to a base manifold 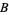 . Any fiber
. Any fiber 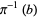 is a space isomorphic to
is a space isomorphic to 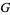 . More specifically,
. More specifically, 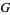 acts freely without fixed point on the fibers, and this makes a fiber into a homogeneous space. For example, in the case of a circle bundle (i.e., when
acts freely without fixed point on the fibers, and this makes a fiber into a homogeneous space. For example, in the case of a circle bundle (i.e., when 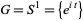 ), the fibers are circles, which can be rotated, although no point in particular corresponds to the identity. Near every point, the fibers can be given the group structure of
), the fibers are circles, which can be rotated, although no point in particular corresponds to the identity. Near every point, the fibers can be given the group structure of 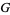 in the fibers over a neighborhood
in the fibers over a neighborhood 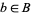 by choosing an element in each fiber to be the identity element. However, the fibers cannot be given a group structure globally, except in the case of a trivial bundle.
by choosing an element in each fiber to be the identity element. However, the fibers cannot be given a group structure globally, except in the case of a trivial bundle.
An important principal bundle is the frame bundle on a Riemannian manifold. This bundle reflects the different ways to give an orthonormal basis for tangent vectors.
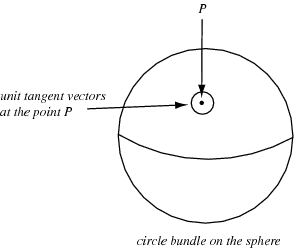
Consider all of the unit tangent vectors on the sphere. This is a principal bundle 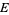 on the sphere with fiber the circle
on the sphere with fiber the circle 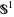 . Every tangent vector projects to its base point in
. Every tangent vector projects to its base point in 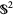 , giving the map
, giving the map 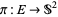 . Over every point in
. Over every point in 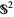 , there is a circle of unit tangent vectors. No particular vector is singled out as the identity, but the group
, there is a circle of unit tangent vectors. No particular vector is singled out as the identity, but the group 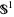 of rotations acts freely without fixed point on the fibers.
of rotations acts freely without fixed point on the fibers.
In a similar way, any fiber bundle corresponds to a principal bundle where the group (of the principal bundle) is the group of isomorphisms of the fiber (of the fiber bundle). Given a principal bundle 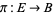 and an action of
and an action of 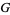 on a space
on a space 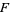 , which could be a group representation, this can be reversed to give an associated fiber bundle.
, which could be a group representation, this can be reversed to give an associated fiber bundle.
A trivialization of a principal bundle, an open set 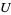 in
in 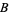 such that the bundle over
such that the bundle over 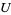 ,
, 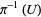 , is expressed as
, is expressed as 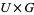 , has the property that the group
, has the property that the group 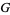 acts on the left. That is,
acts on the left. That is, 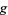 acts on
acts on 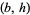 by
by 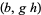 . Tracing through these definitions, it is not hard to see that the transition functions take values in
. Tracing through these definitions, it is not hard to see that the transition functions take values in 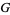 , acting on the fibers by right multiplication. This way the action of
, acting on the fibers by right multiplication. This way the action of 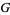 on a fiber is independent of coordinate chart.
on a fiber is independent of coordinate chart.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|