


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-6-2021
Date: 20-6-2021
Date: 5-7-2021
|
A set in 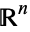 which can be reduced to one of its points, say
which can be reduced to one of its points, say 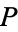 , by a continuous deformation, is said to be contractible. The transformation is such that each point of the set is driven to
, by a continuous deformation, is said to be contractible. The transformation is such that each point of the set is driven to 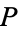 through a path with the properties that
through a path with the properties that
1. Each path runs entirely inside the set.
2. Nearby points move on "neighboring" paths.
Condition (1) implies that a disconnected set, i.e., a set consisting of separate parts, cannot be contractible.
Condition (2) implies that the circumference of a circle is not contractible. The latter follows by considering two near points 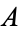 and
and 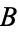 lying on different sides of a point
lying on different sides of a point 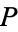 . The paths connecting
. The paths connecting 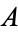 and
and 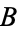 with
with 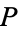 are either opposite each other or have different lengths. A similar argument shows that, in general, for all
are either opposite each other or have different lengths. A similar argument shows that, in general, for all 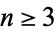 , the
, the 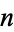 -sphere (i.e., the boundary of the
-sphere (i.e., the boundary of the 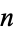 -dimensional ball) is not contractible.
-dimensional ball) is not contractible.
A gap or a hole in a set can be an obstruction to contractibility. There are, however, examples of contractible sets with holes, for example, the "house with two rooms." In a case like this, it is not evident how to construct a transformation of the type described above. However, its existence is assured by the formal definition of contractibility of a set 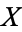 , namely that
, namely that 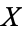 is homotopic to one of its points
is homotopic to one of its points 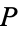 . This means that there is a continuous map
. This means that there is a continuous map ![F:[0,1]×X->X](https://mathworld.wolfram.com/images/equations/Contractible/Inline16.gif) such that
such that 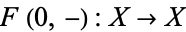 is the identity map and
is the identity map and 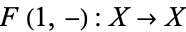 is the constant map sending each point to
is the constant map sending each point to 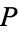 . Thus,
. Thus, 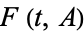 describes a continuous path from
describes a continuous path from 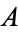 to
to 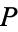 as
as 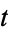 varies from 0 to 1, and (1) is fulfilled. Moreover, since the map
varies from 0 to 1, and (1) is fulfilled. Moreover, since the map 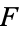 is also continuous with respect to the second component, the path starting at
is also continuous with respect to the second component, the path starting at 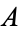 varies continuously with respect to
varies continuously with respect to  , as required by (2).
, as required by (2).
REFERENCES:
Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2002.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|