المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Exponential Factorial |
 889
 03:49 مساءً
date: 1-1-2021 |
Author : Sloane, N. J. A 
Book or Source : Sequences A049384 and A080219 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 16-11-2020
1122
Date: 30-6-2020
604
Date: 5-2-2016
1484
|
The exponential factorial is defined by the recurrence relation
 |
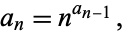(1) |
where 
. The first few terms are therefore
 |
 |
 |
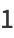(2) |
 |
 |
 |
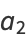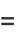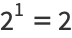(3) |
 |
 |
 |
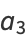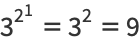(4) |
 |
 |
 |
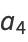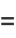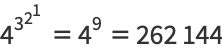(5) |
... (OEIS A049384). The term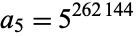 
has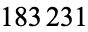 
digits.
The exponential factorial is therefore a kind of "factorial power tower."
The sum of the reciprocals of the exponential factorials is given by
 |
 |
 |
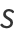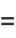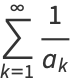(6) |
 |
 |
 |
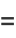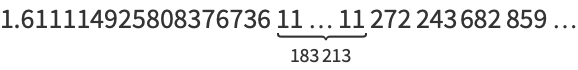(7) |
(OEIS A080219). This sum is a Liouville number and is therefore transcendental.
REFERENCES:
Sloane, N. J. A. Sequences A049384 and A080219 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
