
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2019
Date: 20-1-2021
Date: 30-7-2020
|
That part of a positive integer left after all square factors are divided out. For example, the squarefree part of 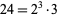 is 6, since
is 6, since 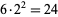 . For
. For 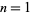 , 2, ..., the first few are 1, 2, 3, 1, 5, 6, 7, 2, 1, 10, ... (OEIS A007913). The squarefree part function can be implemented in the Wolfram Language as
, 2, ..., the first few are 1, 2, 3, 1, 5, 6, 7, 2, 1, 10, ... (OEIS A007913). The squarefree part function can be implemented in the Wolfram Language as
SquarefreePart[n_Integer?Positive] :=
Times @@ Power @@@ ({#[[1]], Mod[#[[2]], 2]}& /@
FactorInteger[n])
REFERENCES:
Atanassov, K. "On the 22nd, 23rd, and the 24th Smarandache Problems. Notes on Number Theory and Discrete Mathematics, Sophia, Bulgaria 5, 80-82, 1999.
Atanassov, K. On Some of the Smarandache's Problems. Lupton, AZ: American Research Press, pp. 16-21, 1999.
Sloane, N. J. A. Sequence A007913 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|