


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-2-2020
Date: 29-1-2020
Date: 21-3-2020
|
A Sierpiński number of the second kind is a number 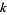 satisfying Sierpiński's composite number theorem, i.e., a Proth number
satisfying Sierpiński's composite number theorem, i.e., a Proth number 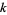 such that
such that 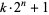 is composite for every
is composite for every 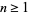 .
.
The smallest known example is 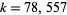 , proved in 1962 by J. Selfridge, but the fate of a number of smaller candidates remains to be determined before this number can be established as the smallest such number. As of 1996, 35 candidates remained (Ribenboim 1996, p. 358), a number which had been reduced to 17 by the beginning of 2002 (Peterson 2003).
, proved in 1962 by J. Selfridge, but the fate of a number of smaller candidates remains to be determined before this number can be established as the smallest such number. As of 1996, 35 candidates remained (Ribenboim 1996, p. 358), a number which had been reduced to 17 by the beginning of 2002 (Peterson 2003).
In March 2002, L. K. Helm and D. A. Norris began a distributed computing effort dubbed "seventeen or bust" to eliminate the remaining candidates. With the aid of collaborators across the globe, this number was reduced to 12 as of December 2003 (Peterson 2003, Helm and Norris). The following table summarizes numbers subsequently found to be prime by "seventeen or bust," leaving only five candidates remaining as of November 2016.
| date | participant | number |
| Dec. 6, 2003 | 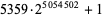 |
|
| Jun. 8, 2005 | D. Gordon | 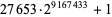 |
| Oct. 15, 2005 | R. Hassler | 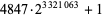 |
| May 5, 2007 | K. Agafonov | 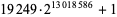 |
| Oct. 30, 2007 | S. Sunde | 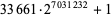 |
| Nov. 6, 2016 | P. Szabolcs | 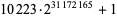 |
The following table lists the known primes together with the only remaining candidates which, as Jan. 2008, are the six numbers 10223, 21181, 22699, 24737, 55459, and 67607. A list of primes found by the project is also maintained by Caldwell (https://primes.utm.edu/bios/page.php?id=429).
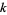 |
prime | digits | Caldwell |
| 4847 | 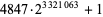 |
999744 | https://primes.utm.edu/primes/page.php?id=75994 |
| 5359 | 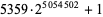 |
1521561 | https://primes.utm.edu/primes/page.php?id=67719 |
| 10223 | 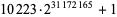 |
9383761 | https://primes.utm.edu/primes/page.php?id=122473 |
| 19249 | 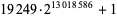 |
3918990 | https://primes.utm.edu/primes/page.php?id=80385 |
| 21181 | |||
| 22699 | |||
| 24737 | |||
| 27653 | 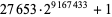 |
2759677 | https://primes.utm.edu/primes/page.php?id=74836 |
| 28433 | 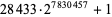 |
2357207 | https://primes.utm.edu/primes/page.php?id=73145 |
| 33661 | 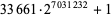 |
2116617 | https://primes.utm.edu/primes/page.php?id=82804 |
| 44131 | 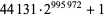 |
299823 | https://primes.utm.edu/primes/page.php?id=62867 |
| 46157 | 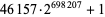 |
210186 | https://primes.utm.edu/primes/page.php?id=62865 |
| 54767 | 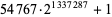 |
402569 | https://primes.utm.edu/primes/page.php?id=62869 |
| 55459 | |||
| 65567 | 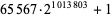 |
305190 | https://primes.utm.edu/primes/page.php?id=62866 |
| 67607 | |||
| 69109 | 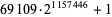 |
348431 | https://primes.utm.edu/primes/page.php?id=62868 |
Consider now restricting Sierpiński numbers of the second kind to those with prime 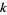 . The smallest proved prime Sierpiński number is 271129. A distributed computing project to find examples of
. The smallest proved prime Sierpiński number is 271129. A distributed computing project to find examples of 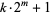 that are prime with
that are prime with 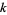 smaller than the proven lower limit is currently underway (Caldwell). Note that the smallest candidates include three prime candidates from the "seventeen or bust" list: 10223, 22699, 67607. A list of primes found by the project is maintained by Caldwell (https://primes.utm.edu/bios/page.php?id=564).
smaller than the proven lower limit is currently underway (Caldwell). Note that the smallest candidates include three prime candidates from the "seventeen or bust" list: 10223, 22699, 67607. A list of primes found by the project is maintained by Caldwell (https://primes.utm.edu/bios/page.php?id=564).
Let 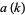 be smallest
be smallest 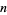 for which
for which 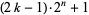 is prime, then the first few values are 0, 1, 1, 2, 1, 1, 2, 1, 3, 6, 1, 1, 2, 2, 1, 8, 1, 1, 2, 1, 1, 2, 2, 583, ... (OEIS A046067). The second smallest
is prime, then the first few values are 0, 1, 1, 2, 1, 1, 2, 1, 3, 6, 1, 1, 2, 2, 1, 8, 1, 1, 2, 1, 1, 2, 2, 583, ... (OEIS A046067). The second smallest 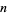 are given by 1, 2, 3, 4, 2, 3, 8, 2, 15, 10, 4, 9, 4, 4, 3, 60, 6, 3, 4, 2, 11, 6, 9, 1483, ... (OEIS A046068). Quite large
are given by 1, 2, 3, 4, 2, 3, 8, 2, 15, 10, 4, 9, 4, 4, 3, 60, 6, 3, 4, 2, 11, 6, 9, 1483, ... (OEIS A046068). Quite large 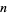 can be required to obtain the first prime even for small
can be required to obtain the first prime even for small 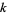 . For example, the smallest prime of the form
. For example, the smallest prime of the form 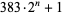 is
is 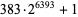 .
.
There are an infinite number of Sierpiński numbers which are prime.
The smallest odd 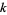 such that
such that 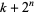 is composite for all
is composite for all 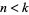 are 773, 2131, 2491, 4471, 5101, ... (OEIS A033919).
are 773, 2131, 2491, 4471, 5101, ... (OEIS A033919).
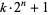 is always composite for
is always composite for 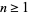 and Gaussian integers
and Gaussian integers 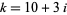 ,
, 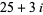 , and
, and 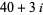 . (E. Pegg Jr., pers. comm., Feb. 6, 2003; Broadhurst 2005).
. (E. Pegg Jr., pers. comm., Feb. 6, 2003; Broadhurst 2005).
REFERENCES:
Baillie, R.; Cormack, G.; and Williams, H. C. "The Problem of Sierpinski Concerning 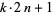 ." Math. Comput. 37, 229-231, 1981.
." Math. Comput. 37, 229-231, 1981.
Ballinger, R. "The Sierpinski Problem: Definition and Status." https://www.prothsearch.net/sierp.html.
Broadhurst, D. "Might Jean Complexify SoB?" primeform group posting. Oct. 30, 2005. https://groups.yahoo.com/group/primeform/message/6620/.
Caldwell, C. "The Prime Sierpinski Problem." https://primes.utm.edu/bios/page.php?id=564.
Caldwell, C. "Seventeen or Bust." https://primes.utm.edu/bios/page.php?id=429.
Buell, D. A. and Young, J. "Some Large Primes and the Sierpiński Problem." SRC Tech. Rep. 88004, Supercomputing Research Center, Lanham, MD, 1988.
Helm, L. Press release upon discovery of 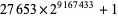 . June 15, 2005. https://www.seventeenorbust.com/documents/press-061505.mhtml.
. June 15, 2005. https://www.seventeenorbust.com/documents/press-061505.mhtml.
Helm, L. Press release upon discovery of 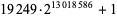 . May 5, 2007. https://www.seventeenorbust.com/documents/press-050507.mhtml.
. May 5, 2007. https://www.seventeenorbust.com/documents/press-050507.mhtml.
Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem." https://www.seventeenorbust.com/.
Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem--Project Statistics." https://www.seventeenorbust.com/stats/.
Jaeschke, G. "On the Smallest 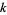 such that
such that 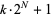 are Composite." Math. Comput. 40, 381-384, 1983.
are Composite." Math. Comput. 40, 381-384, 1983.
Jaeschke, G. Corrigendum to "On the Smallest 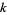 such that
such that 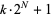 are Composite." Math. Comput. 45, 637, 1985.
are Composite." Math. Comput. 45, 637, 1985.
Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 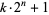 ." Math. Comput. 41, 661-673, 1983.
." Math. Comput. 41, 661-673, 1983.
Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 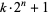 , II." In prep.
, II." In prep.
Peterson, I. "MathTrek: A Remarkable Dearth of Primes." Jan. 13, 2003. https://www.sciencenews.org/20030111/mathtrek.asp.
"The Prime Sierpinski Project." https://www.mersenneforum.org/showthread.php?t=2665.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 357-359, 1996.
Sierpiński, W. "Sur un problème concernant les nombres 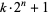 ." Elem. d. Math. 15, 73-74, 1960.
." Elem. d. Math. 15, 73-74, 1960.
Sloane, N. J. A. Sequences A033919, A046067, and A046068 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|