


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2020
Date: 26-8-2020
Date: 24-9-2020
|
Consider the consecutive number sequences formed by the concatenation of the first 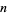 positive integers: 1, 12, 123, 1234, ... (OEIS A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). This sequence gives the digits of the Champernowne constant, and is sometimes also known as the Barbier infinite word (Allouche and Shallit 2003, pp. 114, 299, and 336). The terms up to
positive integers: 1, 12, 123, 1234, ... (OEIS A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). This sequence gives the digits of the Champernowne constant, and is sometimes also known as the Barbier infinite word (Allouche and Shallit 2003, pp. 114, 299, and 336). The terms up to 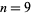 are given by
are given by
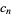 |
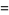 |
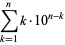 |
(1) |
 |
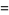 |
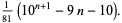 |
(2) |
These are sometimes called Smarandache consecutive numbers, but in this work, the terms in the sequence will be called simply Smarandache numbers. Similarly, a Smarandache number that is prime will be called a Smarandache prime. Surprisingly, no Smarandache primes 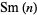 exist for
exist for 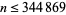 (Great Smarandache PRPrime search; Dec. 5, 2016).
(Great Smarandache PRPrime search; Dec. 5, 2016).
The number of digits of 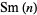 can be computed by noticing the pattern in the following table, where
can be computed by noticing the pattern in the following table, where
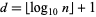 |
(3) |
is the number of digits in 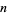 .
.
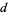 |
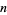 range range |
digits |
| 1 | 1-9 | 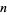 |
| 2 | 10-99 | 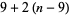 |
| 3 | 100-999 | 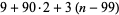 |
| 4 | 1000-9999 | 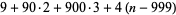 |
By induction, the number of digits 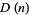 in
in 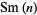 can be written
can be written
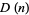 |
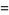 |
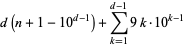 |
(4) |
 |
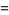 |
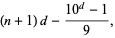 |
(5) |
where the second term is the repunit 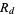 . For
. For 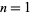 , 2, ..., the digit lengths
, 2, ..., the digit lengths 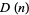 of
of 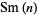 are therefore 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, ... (OEIS A058183).
are therefore 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, ... (OEIS A058183).

The results of concatenating the binary representations of the first few integers are 1, 110, 11011, 11011100, 11011100101, ... (OEIS A058935). These digit sequences are plotted above for 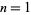 to 90. Interpreting the digit sequence as a binary fraction, the result is the binary Champernowne constant
to 90. Interpreting the digit sequence as a binary fraction, the result is the binary Champernowne constant  .
.
Interestingly, taking the cumulative sum 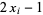 where
where 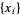 are the digits
are the digits 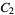 gives a plot showing batrachion-like structure (left figure), and doing the same with
gives a plot showing batrachion-like structure (left figure), and doing the same with 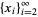 (right figure) gives structures resembling the Blancmange function (and the Hofstadter-Conway $10,000 sequence).
(right figure) gives structures resembling the Blancmange function (and the Hofstadter-Conway $10,000 sequence).
REFERENCES:
--. "The Great Smarandache PRPrime search." https://smarandache.ddns.net:1200/server_stats.html.
Mudge, M. "Top of the Class." Personal Computer World, 674-675, June 1995.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Sloane, N. J. A. Sequences A007908, A058183, and A058935 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Stephan, R. W. "Factors and Primes in Two Smarandache Sequences." Smarandache Notions J. 9, 4-10, 1998.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|