


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-2-2020
Date: 22-11-2019
Date: 6-5-2020
|
Mills' constant can be defined as the least 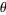 such that
such that
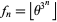 |
is prime for all positive integers 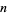 (Caldwell and Cheng 2005).
(Caldwell and Cheng 2005).
The first few 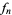 for
for 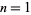 , 2, ... are 2, 11, 1361, 2521008887, ... (OEIS A051254). They can be represented more compactly through
, 2, ... are 2, 11, 1361, 2521008887, ... (OEIS A051254). They can be represented more compactly through 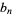 as
as 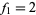 and
and
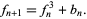 |
Caldwell and Cheng (2005) calculated the first 10 Mills primes. 13 are known as of Jul. 2013, with the firth few 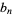 for
for 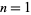 , 2, ... being 3, 30, 6, 80, 12, 450, 894, 3636, 70756, 97220, 66768, 300840, ... (OEIS A108739).
, 2, ... being 3, 30, 6, 80, 12, 450, 894, 3636, 70756, 97220, 66768, 300840, ... (OEIS A108739). 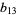 is not known, but it is known that
is not known, but it is known that 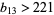 (E. Weisstein, Aug. 13, 2013).
(E. Weisstein, Aug. 13, 2013).
The integer lengths of the Mills' primes are 1, 2, 4, 10, 29, 85, 254, 762, 2285, 6854, 20562, 61684, 185052, ... (OEIS A224845).
REFERENCES:
Caldwell, C. K. and Cheng, Y. "Determining Mills' Constant and a Note on Honaker's Problem." J. Integer Sequences 8, Article 05.4.1, 1-9, 2005. https://www.cs.uwaterloo.ca/journals/JIS/VOL8/Caldwell/caldwell78.html.
Sloane, N. J. A. Sequences A051254, A108739, and A224845 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|