


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-1-2020
Date: 3-8-2020
Date: 12-1-2021
|
The base 2 method of counting in which only the digits 0 and 1 are used. In this base, the number 1011 equals 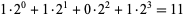 . This base is used in computers, since all numbers can be simply represented as a string of electrically pulsed ons and offs. In computer parlance, one binary digit is called a bit, two digits are called a crumb, four digits are called a nibble, and eight digits are called a byte.
. This base is used in computers, since all numbers can be simply represented as a string of electrically pulsed ons and offs. In computer parlance, one binary digit is called a bit, two digits are called a crumb, four digits are called a nibble, and eight digits are called a byte.
An integer 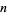 may be represented in binary in the Wolfram Language using the command BaseForm[n, 2], and the first
may be represented in binary in the Wolfram Language using the command BaseForm[n, 2], and the first 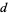 digits of a real number
digits of a real number  may be obtained in binary using RealDigits[x, 2, d]. Finally, a list of binary digits
may be obtained in binary using RealDigits[x, 2, d]. Finally, a list of binary digits 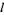 can be converted to a decimal rational number or integer using FromDigits[l, 2].
can be converted to a decimal rational number or integer using FromDigits[l, 2].
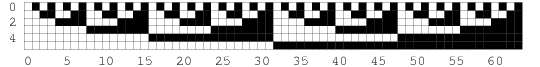
The illustration above shows the binary numbers from 0 to 63 represented graphically (Wolfram 2002, p. 117), and the following table gives the binary equivalents of the first few decimal numbers.
| 1 | 1 | 11 | 1011 | 21 | 10101 |
| 2 | 10 | 12 | 1100 | 22 | 10110 |
| 3 | 11 | 13 | 1101 | 23 | 10111 |
| 4 | 100 | 14 | 1110 | 24 | 11000 |
| 5 | 101 | 15 | 1111 | 25 | 11001 |
| 6 | 110 | 16 | 10000 | 26 | 11010 |
| 7 | 111 | 17 | 10001 | 27 | 11011 |
| 8 | 1000 | 18 | 10010 | 28 | 11100 |
| 9 | 1001 | 19 | 10011 | 29 | 11101 |
| 10 | 1010 | 20 | 10100 | 30 | 11110 |
A negative number 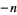 is most commonly represented in binary using the complement of the positive number
is most commonly represented in binary using the complement of the positive number 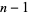 , so
, so 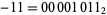 would be written as the complement of
would be written as the complement of 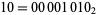 , or 11110101. This allows addition to be carried out with the usual carrying and the leftmost digit discarded, so
, or 11110101. This allows addition to be carried out with the usual carrying and the leftmost digit discarded, so 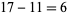 gives
gives
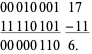 |
The number of times 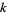 that a given binary number
that a given binary number 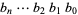 is divisible by 2 is given by the position of the first
is divisible by 2 is given by the position of the first 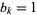 counting from the right. For example,
counting from the right. For example, 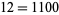 is divisible by 2 twice, and
is divisible by 2 twice, and 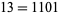 is divisible by 2 zero times. The number of times that 1, 2, ... are divisible by 2 are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, 0, 1, 0, 2, ... (OEIS A007814), which is the binary carry sequence.
is divisible by 2 zero times. The number of times that 1, 2, ... are divisible by 2 are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, 0, 1, 0, 2, ... (OEIS A007814), which is the binary carry sequence.
Real numbers can also be represented using binary notation by interpreting digits past the "decimal" point as negative powers of two, so the binary digits 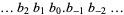 would represent the number
would represent the number
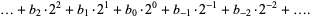 |
Therefore, 1/2 would be represented as 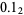 , 1/4 as
, 1/4 as 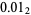 , 3/4 as
, 3/4 as 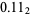 , and so on. The sequence of binary digits for the integers
, and so on. The sequence of binary digits for the integers 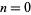 , 1, ... concatenated together and interpreted as a binary constant give the binary Champernowne constant
, 1, ... concatenated together and interpreted as a binary constant give the binary Champernowne constant 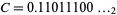 (OEIS A030190).
(OEIS A030190).
Unfortunately, the storage of binary numbers in computers is not entirely standardized. Because computers store information in 8-bit bytes (where a bit is a single binary digit), depending on the "word size" of the machine, numbers requiring more than 8 bits must be stored in multiple bytes. The usual FORTRAN77 integer size is 4 bytes long. However, a number represented as (byte1 byte2 byte3 byte4) in a VAX would be read and interpreted as (byte4 byte3 byte2 byte1) on a Sun. The situation is even worse for floating-point (real) numbers, which are represented in binary as a mantissa and characteristic, and worse still for long (8-byte) reals!
Binary multiplication of single bit numbers (0 or 1) is equivalent to the AND operation, as can be seen in the following multiplication table.
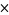 |
0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
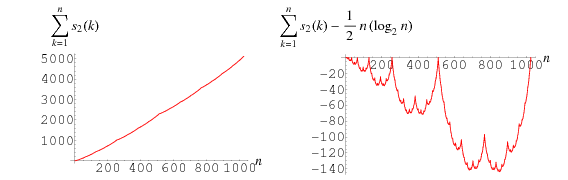
Consider the cumulative digit sum of all binary numbers up to 1, 2, ..., 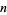 . The first few terms are then 1, 2, 4, 5, 7, 9, 12, 13, 15, 17, 20, 22, ... (OEIS A000788). This sequence in monotonic increasing (left figure), but if the main asymptotic term is removed, a sequence of humped curves (right figure; Trott 2004, p. 218) tending towards the Blancmange function is obtained.
. The first few terms are then 1, 2, 4, 5, 7, 9, 12, 13, 15, 17, 20, 22, ... (OEIS A000788). This sequence in monotonic increasing (left figure), but if the main asymptotic term is removed, a sequence of humped curves (right figure; Trott 2004, p. 218) tending towards the Blancmange function is obtained.
REFERENCES:
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Factorial Factors." §4.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 111-115, 1994.
Heath, F. G. "Origin of the Binary Code." Sci. Amer. 227, 76-83, Aug. 1972.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 6-9, 1991.
Pappas, T. "Computers, Counting, & Electricity." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 24-25, 1989.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Error, Accuracy, and Stability" and "Diagnosing Machine Parameters." §1.2 and §20.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 18-21, 276, and 881-886, 1992.
Sloane, N. J. A. Sequences A000788/M0964, A007814, and A030190 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 42-44, 1986.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 117, 2002.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|