


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-8-2020
Date: 20-8-2020
Date: 6-10-2020
|
Apply the 196-algorithm, which consists of taking any positive integer of two digits or more, reversing the digits, and adding to the original number. Now sum the two and repeat the procedure with the sum. Of the first 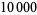 numbers, only 251 do not produce a palindromic number in
numbers, only 251 do not produce a palindromic number in 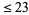 steps (Gardner 1979).
steps (Gardner 1979).
It was therefore conjectured that all numbers will eventually yield a palindromic number. However, the conjecture has been proven false for bases which are a power of 2, and seems to be false for base 10 as well. Among the first 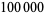 numbers,
numbers, 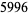 numbers apparently never generate a palindromic number (Gruenberger 1984). The first few are 196, 887, 1675, 7436, 13783, 52514, 94039, 187088, 1067869, 10755470, ... (OEIS A006960).
numbers apparently never generate a palindromic number (Gruenberger 1984). The first few are 196, 887, 1675, 7436, 13783, 52514, 94039, 187088, 1067869, 10755470, ... (OEIS A006960).
It is conjectured, but not proven, that there are an infinite number of palindromic primes. With the exception of 11, palindromic primes must have an odd number of digits.
REFERENCES:
Gardner, M. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 242-245, 1979.
Gruenberger, F. "How to Handle Numbers with Thousands of Digits, and Why One Might Want to." Sci. Amer. 250, 19-26, Apr. 1984.
Sloane, N. J. A. Sequence A006960/M5410 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|