المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Silverman,s Sequence |
 847
 04:53 مساءً
date: 4-11-2020 |
Author : Sloane, N. J. A. 
Book or Source : Sequence A001462/M0257 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 12-5-2020
844
Date: 8-5-2020
859
Date: 9-11-2020
957
|
Let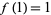 
, and let 
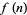be the number of occurrences of 
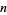in a nondecreasing sequence of integers. then the first few values of 
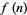are 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, ... (OEIS A001462). the asymptotic value of the 
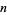th term is 
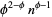, where 
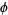is the golden ratio.
REFERENCES:
Guy, R. K. "Silverman's Sequences." §E25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 225-226, 1994.
Sloane, N. J. A. Sequence A001462/M0257 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|
