المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Near Noble Number |
 848
 05:38 مساءً
date: 8-5-2020 |
Author : Schroeder, M. R. 
Book or Source : Number Theory in Science and Communication: With Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity, 2nd enl.... 
Page and Part : ...|
Read More
Date: 30-11-2019
1042
Date: 9-9-2020
823
Date: 21-1-2021
1161
|
A near noble number is a real number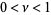 
whose continued fraction is periodic, and the periodic sequence of terms is composed of a string of 
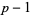1s followed by an integer 
,
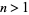![nu_(p,n)=[0,1,1,...,1_()_(p-1),n^_].](https://mathworld.wolfram.com/images/equations/NearNobleNumber/NumberedEquation1.gif) |
(1) |
This can be written in the form
![nu_(p,n)=[0,1,1,...,1_()_(p-1),n,nu_(p,n)^(-1)],](https://mathworld.wolfram.com/images/equations/NearNobleNumber/NumberedEquation2.gif) |
(2) |
which can be solved to give
 |
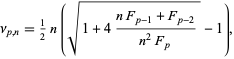(3) |
where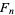 
is a Fibonacci number.
Special cases include
 |
 |
 |
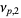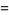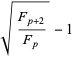(4) |
 |
 |
 |
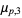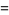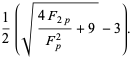(5) |
REFERENCES:
Schroeder, M. R. Number Theory in Science and Communication: With Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity, 2nd enl. ed., corr. printing. Berlin: Springer-Verlag, 1990.
Schroeder, M. "Noble and Near Noble Numbers." In Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, pp. 392-394, 1991.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|
