


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-10-2020
Date: 24-10-2019
Date: 14-11-2019
|
A sequence of real numbers 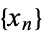 is equidistributed on an interval
is equidistributed on an interval ![[a,b]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline2.gif) if the probability of finding
if the probability of finding 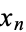 in any subinterval is proportional to the subinterval length. The points of an equidistributed sequence form a dense set on the interval
in any subinterval is proportional to the subinterval length. The points of an equidistributed sequence form a dense set on the interval ![[a,b]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline4.gif) .
.
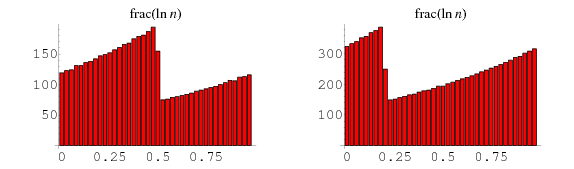
However, dense sets need not necessarily be equidistributed. For example, 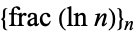 , where
, where 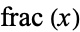 is the fractional part, is dense in
is the fractional part, is dense in ![[0,1]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline7.gif) but not equidistributed, as illustrated above for
but not equidistributed, as illustrated above for 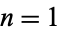 to 5000 (left) and
to 5000 (left) and 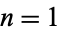 to
to 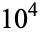 (right)
(right)
Hardy and Littlewood (1914) proved that the sequence 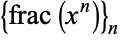 , of power fractional parts is equidistributed for almost all real numbers
, of power fractional parts is equidistributed for almost all real numbers 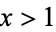 (i.e., the exceptional set has Lebesgue measure zero). Exceptional numbers include the positive integers, the silver ratio
(i.e., the exceptional set has Lebesgue measure zero). Exceptional numbers include the positive integers, the silver ratio 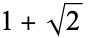 (Finch 2003), and the golden ratio
(Finch 2003), and the golden ratio 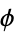 .
.
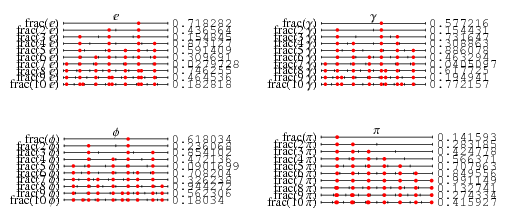
The top set of above plots show the values of 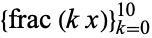 for
for 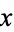 equal to e, the Euler-Mascheroni constant
equal to e, the Euler-Mascheroni constant 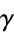 , the golden ratio
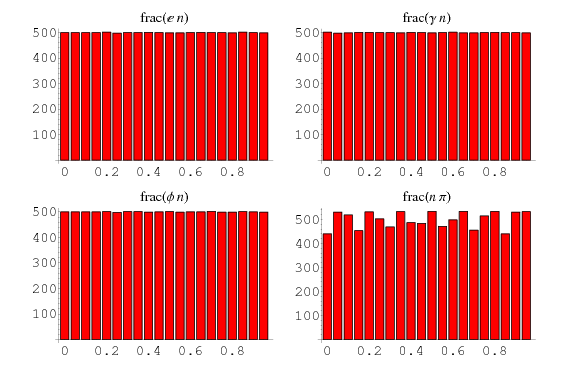
, the golden ratio 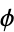 , and pi. Similarly, the bottom set of above plots show a histogram of the distribution of
, and pi. Similarly, the bottom set of above plots show a histogram of the distribution of 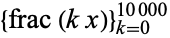 for these constants. Note that while most settle down to a uniform-appearing distribution,
for these constants. Note that while most settle down to a uniform-appearing distribution, 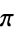 curiously appears nonuniform after
curiously appears nonuniform after 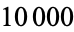 iterations. Steinhaus (1999) remarks that the highly uniform distribution of
iterations. Steinhaus (1999) remarks that the highly uniform distribution of 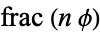 has its roots in the form of the continued fraction for
has its roots in the form of the continued fraction for 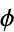 .
.
Now consider the number of empty intervals in the distribution of 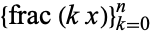 in the intervals bounded by the intervals determined by 0,
in the intervals bounded by the intervals determined by 0, 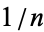 ,
, 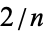 , ...,
, ..., 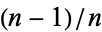 , 1 for
, 1 for 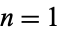 , 2, ..., summarized below for the constants previously considered.
, 2, ..., summarized below for the constants previously considered.
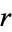 |
Sloane | # empty intervals for 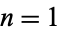 , 2, ... , 2, ... |
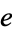 |
A036412 | 0, 0, 0, 0, 1, 0, 0, 1, 1, 3, 1, 4, 4, 7, 5, ... |
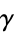 |
A046157 | 0, 0, 0, 1, 0, 0, 0, 1, 2, 2, 3, 0, 3, 5, 3, ... |
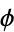 |
A036414 | 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, ... |
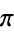 |
A036416 | 0, 1, 1, 1, 1, 0, 0, 1, 2, 3, 4, 4, 5, 7, 7, ... |
The values of 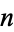 for which no bins are left blank are given in the following table.
for which no bins are left blank are given in the following table.
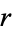 |
Sloane | 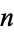 with no empty intervals with no empty intervals |
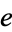 |
A036413 | 1, 2, 3, 4, 6, 7, 32, 35, 39, 71, 465, 536, 1001, ... |
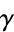 |
A046158 | 1, 2, 3, 5, 6, 7, 12, 19, 26, 97, 123, 149, 272, 395, ... |
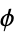 |
A036415 | 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, ... |
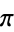 |
A036417 | 1, 6, 7, 106, 112, 113, 33102, 33215, ... |
REFERENCES:
Hardy, G. H. and Littlewood, J. E. "Some Problems of Diophantine Approximation." Acta Math. 37, 193-239, 1914.
Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.
Pólya, G. and Szegö, G. Problems and Theorems in Analysis I. New York: Springer-Verlag, p. 88, 1972.
Sloane, N. J. A. Sequences A036412, A036413, A036414, A036415, A036416, A036417, A046157, and A046158 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 155-156, 1991.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|