


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-10-2019
Date: 13-9-2020
Date: 8-12-2020
|
The Copeland-Erdős constant is the constant with decimal expansion 0.23571113171923... (OEIS A033308) obtained by concatenating consecutive primes: 2, 23, 235, 2357, 235711, ... (OEIS A019518). It is one of the Smarandache sequences and is considered as an infinite word by Allouche and Shallit (2003, pp. 299 and 334).
It is therefore given by the formula
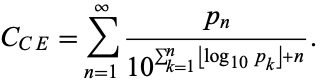 |
Copeland and Erdős (1946) showed that it is a normal number in base 10.
Interestingly, while the Champernowne constant continued fraction contains sporadic very large terms, making the continued fraction difficult to calculate, the Copeland-Erdős constant continued fraction is well-behaved and does not show the "large term" phenomenon.
REFERENCES:
Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Champernowne, D. G. "The Construction of Decimals Normal in the Scale of Ten." J. London Math. Soc. 8, 1933.
Copeland, A. H. and Erdős, P. "Note on Normal Numbers." Bull. Amer. Math. Soc. 52, 857-860, 1946.
Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, p. 284, 2002.
Sloane, N. J. A. Sequences A019518, A030168, A033308, A033309, A033310, and A224890 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|