Power Floors

The sequence 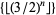 is given by 1, 1, 2, 3, 5, 7, 11, 17, 25, 38, ... (OEIS A002379). The first few composite  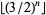occur for 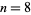, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 23, ... (OEIS A046037), corresponding to the composites 25, 38, 57, 86, 129, 194, 291, 437, 656, ... (OEIS A070758). Similarly, the first few prime  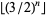occur for 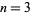, 4, 5, 6, 7, 21, 22, 98, ... (OEIS A070759), corresponding to the primes 2, 3, 5, 7, 11, 17, 4987, 7481, 180693856682317883, ... (OEIS A067904).

The sequence 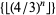 is given by 1, 1, 2, 3, 4, 5, 7, 9, 13, 17, 23, ... (OEIS A064628). The first few composite  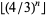occur for 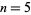, 8, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, ... (OEIS A046038), corresponding to composites 4, 9, 42, 56, 74, 99, 133, 177, 236, ... (OEIS A070761). Similarly, the first few prime  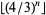occur for 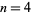, 6, 7, 9, 10, 11, 12, 38, 42, 59, 96,... (OEIS A070762), corresponding to the primes 2, 3, 5, 7, 13, 17, 23, 31, 55933, 176777, 23517191, ... (OEIS A067905).

There are infinitely many integers of the form 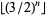 and 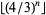 which are composite, where  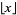is the floor function (Forman and Shapiro, 1967; Guy 1994, p. 220).

REFERENCES:

Forman, W. and Shapiro, H. N. "An Arithmetic Property of Certain Rational Powers." Comm. Pure Appl. Math. 20, 561-573, 1967.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.

Sloane, N. J. A. Sequences A002379/M0666, A046037, A046038, A064628, A067904, A067905, A070758, A070759, A070761, and A070762 in "The On-Line Encyclopedia of Integer Sequences."