Riesel Number

There exist infinitely many odd integers 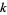 such that  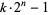is composite for every 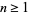. Numbers  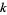with this property are called Riesel numbers, while analogous numbers with the minus sign replaced by a plus are called Sierpiński numbers of the second kind.

The smallest known Riesel number is 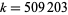, but as of Jan. 2014, there remain 52 smaller candidates which generate only composite numbers for all  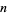which have been checked (Ribenboim 1996, p. 358; Ballinger and Keller; Keller): 2293, 9221, 23669, 31859, 38473, 46663, 67117, 74699, 81041, 93839, 97139, 107347, 121889, 129007, 143047, 146561, 161669, 192971, 206039, 206231, 215443, 226153, 234343, 245561, 250027, 273809, 315929, 319511, 324011, 325123, 327671, 336839, 342847, 344759, 362609, 363343, 364903, 365159, 368411, 371893, 384539, 386801, 397027, 402539, 409753, 444637, 470173, 474491, 477583, 485557, 494743, and 502573.

The problem of proving or disproving that 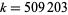 is the smallest Riesel number is sometimes known as the Riesel problem or Riesel conjecture.

Let 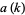 be smallest  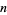for which  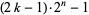is prime, then the first few values are 2, 0, 2, 1, 1, 2, 3, 1, 2, 1, 1, 4, 3, 1, 4, 1, 2, 2, 1, 3, 2, 7, ... (OEIS A046069), and second smallest  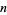are 3, 1, 4, 5, 3, 26, 7, 2, 4, 3, 2, 6, 9, 2, 16, 5, 3, 6, 2553, ... (OEIS A046070).

Primes of the form 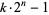 discovered to date providing disproof of the existence of smaller Riesel numbers are summarized in the following table (Keller).

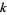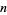		Discoverer	Date
659	800516	Dave Linton	01 Mar 2004
26773	2465343	Anonymous & RSP	01 Dec 2006
27253	272347	Ray Ballinger	10 Oct 1998
39269	287048	Richard Heylen	25 Mar 2002
40597	6808509	Frank Meador	25 Dec 2013
42779	322908	Ray Ballinger	26 Jul 1999
43541	507098	Ray Ballinger	01 Oct 2000
46271	428210	Patrick Pirson	29 Apr 2001
65531	3629342	Adrian Schori & PrimeGrid	05 Apr 2011
71009	1185112	Drew Bishop & RSP	05 Dec 2004
89707	578313	Richard Heylen	02 Apr 2003
93997	864401	Guido Stolz & RSP	01 Apr 2004
98939	575144	Olivier Haeberlé	30 Nov 2001
103259	615076	Olivier Haeberlé	23 Dec 2002
104917	340181	Janusz Szmidt	13 Nov 1999
109897	630221	Olivier Haeberlé	22 Apr 2003
110413	1591999	Will Fisher & RSP	08 Jun 2005
113983	3201175	Ian Keogh & RSP	01 May 2008
114487	2198389	Bruce White & RSP	23 May 2006
123547	3804809	Jakub Łuszczek & PrimeGrid	08 May 2011
126667	626497	Ray Ballinger	09 Jun 2003
130139	280296	Dale Andrews	02 Feb 2002
141941	4299438	Scott Brown & PrimeGrid	26 May 2011
144643	498079	Richard Heylen	12 Dec 2000
148901	360338	Mark Rodenkirch	05 Mar 2002
149797	1414137	Peter van Hoof & RSP	13 Mar 2005
150847	1076441	Darren Wallace & RSP	15 Aug 2004
152713	1154707	Ray Ballinger	23 Oct 2004
159371	284166	Janusz Szmidt	14 Jan 2002
170591	866870	Drew Bishop & RSP	15 Apr 2004
189463	324103	Dave Linton	15 Jul 2000
191249	3417696	Jonathan Pritchard & PrimeGrid	21 Nov 2010
192089	1395688	Guido Stolz & RSP	10 May 2004
196597	2178109	Auritania Du & RSP	09 May 2006
201193	457615	Daval Davis	03 Feb 2003
204223	696891	Olivier Haeberlé	23 Mar 2003
212893	730387	Olivier Haeberlé	15 Oct 2003
215503	649891	Olivier Haeberlé	28 Apr 2003
220033	719731	Olivier Haeberlé	19 Apr 2004
220063	306335	Olivier Haeberlé	03 Sep 1999
222997	613153	Olivier Haeberlé	28 Nov 2001
234847	1535589	Darren Wallace & RSP	09 May 2005
235601	295338	Helmut Zeisel	06 Mar 2003
245051	285750	Tom Kuechler	15 Nov 2000
246299	752600	Kevin O'Hare & RSP	23 Jan 2004
252191	5497878	Jan Haller & PrimeGrid	23 Jun 2012
261221	689422	Sean Faith & RSP	22 Dec 2003
267763	264115	Dave Linton	19 Feb 2000
275293	2335007	Japke Rosink & RSP	21 Sep 2006
277153	429819	Jeff Wolfe	21 Nov 2002
279703	616235	Dhumil Zaveri & RSP	07 Jan 2004
299617	428917	Dave Linton	22 Jul 2002
304207	6643565	Randy Ready & PrimeGrid	11 Oct 2013
309817	901173	Helmut Michel & RSP	07 Jun 2004
325627	1472117	Will Fisher & RSP	05 Apr 2005
342673	2639439	Dhumil Zaveri & RSP	28 Apr 2007
345067	1876573	Dave Linton	13 Nov 2005
350107	1144101	Sean Faith & RSP	24 Oct 2004
353159	4331116	Jaakko Reinman & PrimeGrid	31 May 2011
357491	609338	Lucas Schmid	17 Jan 2003
357659	1779748	Drew Bishop & RSP	25 Sep 2005
376993	293603	Reto Keiser	08 Sep 2002
382691	431722	Ray Ballinger	27 Feb 2003
398023	6418059	Vladimir Volynsky & PrimeGrid	05 Oct 2013
398533	419107	Dave Linton	04 Sep 2002
401143	532927	Olivier Haeberlé	11 Jun 2003
401617	470149	Dave Linton	27 Dec 2002
412717	1084409	Holger Meissner & RSP	22 Aug 2004
415267	3771929	Alexey Tarasov & PrimeGrid	08 May 2011
416413	424791	Dave Linton	28 Apr 2003
417643	1800787	Greg Childers & RSP	05 Oct 2004
428639	3506452	Brett Melvold & PrimeGrid	14 Jan 2011
443857	369457	Nuutti Kuosa	27 Aug 2001
450457	2307905	Jeff Smith & RSP	28 Mar 2006
458743	547791	Olivier Haeberlé	22 Oct 2003
460139	779536	Drew Bishop & RSP	26 Mar 2004
465869	497596	Lucas Schmid	27 Jan 2003
467917	1993429	Steven Wong & RSP	25 Dec 2005
469949	1649228	Steven Wong & RSP	28 Oct 2007
485767	3609357	Chris Cardall & RSP	24 Jun 2008
500621	1138518	Darren Wallace & RSP	18 Oct 2004
502541	1199930	Ryan Sefko & RSP	21 Dec 2004
504613	1136459	Magnus Mischel & RSP	17 Oct 2004

REFERENCES:

Ballinger, R. and Keller, W. "The Riesel Problem: Search for Remaining Candidates." https://www.prothsearch.net/rieselsearch.html.

Keller, W. "The Riesel Problem: Definition and Status." https://www.prothsearch.net/rieselprob.html.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 357, 1996.

Riesel, H. "Några stora primtal." Elementa 39, 258-260, 1956.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Basel: Birkhäuser, pp. 394-398, 1994.

Riesel Sieve Project. "The Riesel Sieve Project: A Distributed Effort to Prove the Riesel Conjecture." https://www.rieselsieve.com/.

Sloane, N. J. A. Sequences A046067, A046068, A046069, and A046070 in "The On-Line Encyclopedia of Integer Sequences."