المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Taniguchi,s Constant |
 552
 02:07 صباحاً
date: 6-10-2020 |
Author : Finch, S 
Book or Source : "Class Number Theory." https://algo.inria.fr/csolve/clss.pdf. May 6, 2005. 
Page and Part : ...|
Read More
Date: 1-1-2020
1430
Date: 29-10-2020
604
Date: 22-4-2020
643
|
Taniguchi's constant is defined as
 |
 |
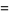![product_(p)[1-3/(p^3)+2/(p^4)+1/(p^5)-1/(p^6)]](https://mathworld.wolfram.com/images/equations/TaniguchisConstant/Inline3.gif) |
(1) |
 |
 |
 |
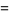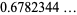(2) |
(OEIS A175639), where the product is over the primes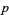 
. Taking the logarithm, expand the sum about infinity, and then summing the terms gives a "closed" form as
 |
 |
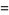![exp[sum_(n=3)^(infty)c_nP(n)]](https://mathworld.wolfram.com/images/equations/TaniguchisConstant/Inline10.gif) |
(3) |
 |
 |
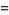![exp[-3P(3)+2P(4)+P(5)-(11)/2P(6)+6P(7)+...],](https://mathworld.wolfram.com/images/equations/TaniguchisConstant/Inline13.gif) |
(4) |
where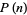 
is the prime zeta function and the 
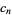s are rational numbers given as the coefficients of 
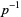in the series
 |
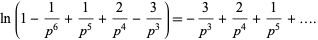(5) |
REFERENCES:
Finch, S. "Class Number Theory." https://algo.inria.fr/csolve/clss.pdf. May 6, 2005.
Sloane, N. J. A. Sequence A175639 in "The On-Line Encyclopedia of Integer Sequences."
Taniguchi, T. "A Mean Value Theorem for the Square of Class Number Times Regulator of Quadratic Extensions." https://arxiv.org/abs/math/0410531. 3 Jul 2006.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
